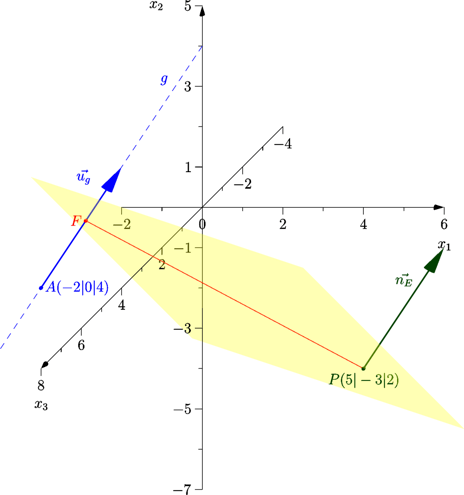
Welchen Abstand hat der Punkt P(5|-3|2) von der Geraden g: 
X
=
−
2
0
4
+
λ
 
1
2
−
2
?
Der Abstand zwischen P und g ist als Länge der senkrechten Verbindungsstrecke von P zur Geraden g zu verstehen.
Lösungsmöglichkeit 1: mittels Hilfsebene
Idee:
1. Führe eine Hilfsebene E ein, die P enthält und senkrecht zu g verläuft. Jede Gerade in der Ebene liegt dann senkrecht zu g.
2. Bestimme den Schnittpunkt (Lotfußpunkt F) von g und E.
3. Berechne die Länge des Verbindungsvektors 
PF
.
graphik
1. Schritt: Ebenengleichung aufstellen
Da g senkrecht zur Ebene stehen soll, wählen wir den Richtungsvektor der Geraden als Normalenvektor der Ebene.
Da P in der Ebene liegen soll, wählen wir den Ortsvektor von P als Aufpunkt der Ebene.
Damit lautet die Normalen- bzw. Koordinatengleichung der Ebene:
X
−
P
·
u
g
=
0
X
−
5
−
3
2
·
1
2
−
2
=
0
x
1
+
2x
2
−
2x
3
−
5
·
1
+
−
3
·
2
+
2
·
−
2
=
0
E: x
1
+
2x
2
−
2x
3
+
5
=
0
2. Schritt: Lotfußpunkt berechnen
Für den Schnittpunkt der Geraden g mit der Ebene E wird g "koordinatenweise" in E eingesetzt, dies ist blau markiert. Die entstehende Gleichung kann nach λ aufgelöst werden.
−
2
+
λ
·
1
+
2
·
0
+
λ
·
2
−
2
·
4
+
λ
·
−
2
+
5
=
0
−
2
+
λ
+
4λ
−
8
+
4λ
+
5
=
0
9λ
−
5
=
0
+
5
9λ
=
5
:9
λ
=
5
9
λ in g einsetzen liefert den Lotfußpunkt F:
F
=
−
2
0
4
+
 
5
9
·
1
2
−
2
=
−
13
9
10
9
26
9
bzw. F(
−
1
4
9
 | 
1
1
9
 | 
2
8
9
)
3. Schritt: Länge des Verbindungsvektors 
PF
 berechnen.
PF
=
−
13
9
−
5
10
9
−
−
3
26
9
−
2
=
−
58
9
37
9
8
9
PF
=
−
58
9
2
+
37
9
2
+
8
9
2
=
4797
81
=
533
9
=
1
3
 
·
533
Der Abstand von P zur Geraden g beträgt damit 
1
3
 
·
533
 
≈ 7,7
.
---------------
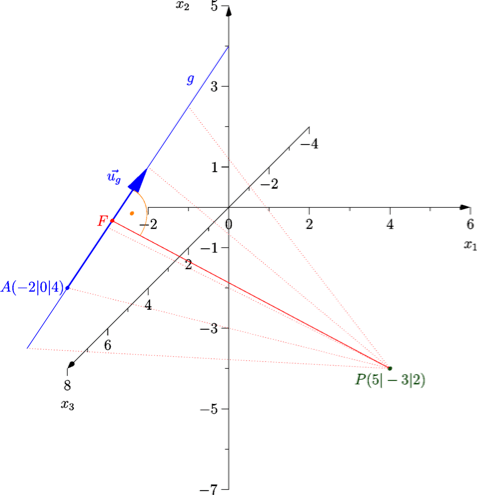
Lösungsmöglichkeit 2: mittels Verbindungsvektor
Idee:
1. Ermittle den Verbindungsvektor von P zu einem beliebigen Punkt 
F
λ
 auf der Geraden (der vom Parameter λ abhängt!).
2. Suche denjenigen Punkt F, für den der Verbindungsvektor senkrecht zur Geraden ist: Das Skalarprodukt von 
PF
λ
 und 
u
g
 ist in diesem Fall gleich Null.
3. Berechne die Länge des senkrechten Verbindungsvektors.
graphik
1. Schritt: Verbindungsvektor 
PF
λ
 bestimmen.
F
λ
 ( -2+λ | 2λ | 4-2λ )
PF
λ
=
−
2
+
λ
−
5
2λ
−
−
3
4
−
2λ
−
2
=
−
7
+
λ
3
+
2λ
2
−
2λ
2. Schritt: Skalarprodukt gleich Null setzen
PF
λ
 
·
 
u
g
=
0
−
7
+
λ
3
+
2λ
2
−
2λ
 
·
 
1
2
−
2
=
0
−
7
+
λ
+
6
+
4λ
−
4
+
4λ
=
0
zusammenfassen
−
5
+
9λ
=
0
+
5
9λ
=
5
:9
λ
=
5
9
Jetzt geht es weiter wie im Lösungsvorschlag 1: λ in g einsetzen liefert denjenigen Geradenpunkt F, dessen Verbindungsvektor mit P senkrecht zu g steht. Dessen Länge liefert den gesuchten Abstand von P zu g.
Koordinatengeometrie im Raum, Abstand Punkt Gerade, Beispiel
Lernvideo

Koordinatengeometrie im Raum, Abstand Punkt Gerade, Beispiel

Kanal: Mathegym