Proportionalität
Eigenschaften von Funktionenscharen in Abhängigkeit vom Scharparameter; Bestimmung des Scharparameters; Schar der Tangenten im Punkt (a|f(a))
(Direkt) proportional heißt: Wenn man die eine Größe verdoppelt/verdreifacht/vervierfacht usw., dann verdoppelt/verdreifacht/vervierfacht usw. sich auch die andere Größe.
Beispiel
Sind folgende Größen jeweils proportional?
a) x=Fahrzeit, y=zurückgelegte Strecke (bei konstanter Geschwindigkeit 75 km/h)
b) x=Anzahl Maler, y=bemalte Fläche pro Stunde
c) x=Seitenlänge eines Quadrats, y=Flächeninhalt des Quadrats
Proportional heißt: Wenn man die eine Größe (x) verdoppelt, verdoppelt sich auch die andere (y). Wenn man x verdreifacht, verdreifacht sich auch y u.s.w.. Da der Quotient aus y und x konstant ist, spricht man von Quotientengleichheit. Den konstanten Quotientenwert y : x nennt man Proportionalitätsfaktor.
Umgekehrt (indirekt, anti-) proportional heißt: Wenn man x verdoppelt, halbiert sich y. Wenn man x verdreifacht, verringert sich y auf den dritten Teil u.s.w.. Da das Produkt aus x und y konstant ist, spricht man von Produktgleichheit.
Beispiel 1
Stelle fest, ob der Zusammenhang zwischen den folgenden Größen jeweils indirekt (synonym: umgekehrt/anti-) proportional ist:
a) x=Geschwindigkeit eines Autos | y=Fahrzeit für eine bestimmte Strecke
b) x=Anzahl der Maler | y=Arbeitsdauer für das Streichen einer Wohnung
c) x=Anzahl der bereits gelesenen Seiten | y=noch ungelesene Seiten eines Buches
Beispiel 2
Die Größen x und y stehen in einem umgekehrt proportionalen (antiproportionalem) Zusammenhang. Fülle die Tabelle vollständig aus.
|
|
|
|
| ||||||||||||||
|
|
|
|
|
Beispiel 3
Natalie beginnt einen Roman, der 330 Seiten umfasst. Nach eine Dreiviertelstunde ist sie auf Seite 21. Überschlage, wie lange sie für das ganze Buch benötigen wird.
Beispiel 4
Prüfe, ob der Zusammenhang proportional, umgekehrt proportional (antiproportional) oder weder noch ist. Gib in den ersten beiden Fällen den noch fehlenden Tabellenwert an.
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
Beispiel 5
Prüfe, ob der Zusammenhang proportional ist. Wenn ja, gib den Proportionalitätsfaktor q an.
|
|
|
| |||||||||||||
|
|
|
|
Beispiel 6
Die Größen x und y stehen in einem proportionalen Zusammenhang. Fülle die Tabelle vollständig aus.
|
|
|
|
| ||||||||||
|
|
|
|
|
Jede Wertetabelle lässt sich grafisch umsetzen, indem man die einzelnen Spalten als Punkte mit entsprechender x- und y-Koordinate liest.
Merke:- Bei Proportionalität ergibt sich eine Gerade, die durch den Ursprung des Koordinatensystems geht.
- Bei umgekehrter Proportionalität (Antiproportionalität) ergibt sich eine sogenannte Hyperbel, deren Äste sich auf die x- und y-Achse zubewegen.
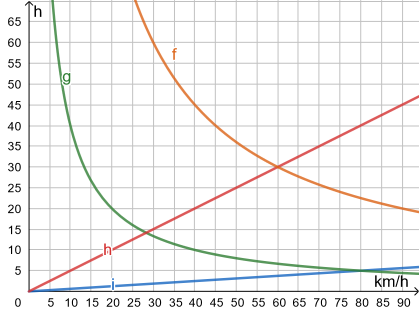
Beispiel
Welcher Graph beschreibt den Zusammenhang zwischen der Fahrzeit und der durchschnittlichen Geschwindigkeit bei einer Strecke von 400 km?