Geometrie - Winkel (II)
Bestimmung einzelner Winkel (Neben-, Scheitel-, Stufen- und Wechselwinkel) an Geraden- und Parallelenkreuzungen, in Dreiecken und in Figuren mit mehr als drei Ecken; Innenwinkelsumme im Dreieck und in Vielecken
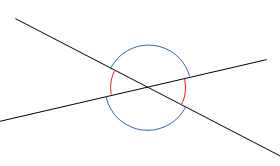
Schneiden sich zwei Geraden, so entstehen vier Winkel mit Scheitel im Schnittpunkt. Jeweils zwei gleichgroße Winkel liegen sich gegenüber - man nennt sie Scheitelwinkel. Zwei benachbarte Winkel hingegen nennt man Nebenwinkel - sie ergänzen sich zu 180°.

Die Summe aller Innenwinkel im Dreieck beträgt 180°. Sind zwei Innenwinkel bekannt, berechnet man den dritten, indem man die angegebenen Winkel von 180° abzieht.
Beispiel
| = | 124° |
γ | = | ?° |
Die Summe aller Innenwinkel im Viereck beträgt 360°. Sind drei Innenwinkel bekannt, berechnet man den vierten, indem man die angegebenen Winkel von 360° abzieht.
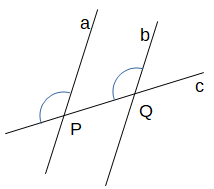
Werden zwei parallele Geraden a und b von einer dritten Gerade c geschnitten, so ergeben sich zwei Schnittpunkte P und Q. Diese sind jeweils Scheitel von vier Winkeln. Ein Winkel mit Scheitel P und ein Winkel mit Scheitel Q heißen:
- Stufenwinkel, wenn sie sich auf derselben Seite von c befinden und wenn sie bzgl. der Parallelen a und b ebenfalls auf derselben Seite liegen, wie z.B. hier:
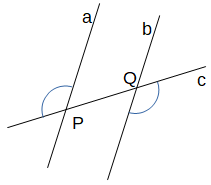
- Wechselwinkel, wenn sie bzgl. c und bzgl. der Parallelen a und b auf unterschiedlichen Seiten liegen, wie z.B. hier:
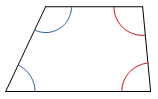
In jedem Trapez treten Paare von Winkeln auf, die sich zu 180° ergänzen.

In jedem achsensymmetrischen Dreieck sind (mindestens) zwei Winkel gleich groß.
In einem gleichschenkligen Dreieck sind die Basiswinkel gleich groß.
- Kennt man den Basiswinkel, so erhält man den Winkel gegenüber der Basis, indem man von 180° das Doppelte des Basiswinkels abzieht.
- Kennt man dagegen den Winkel gegenüber der Basis, so muss man diesen von 180° abziehen und das Ergebnis halbieren, um den Basiswinkel zu bestimmen.
Um einen bestimmten Winkel in einer komplizierten Figur zu berechnen, benötigst du oft mehrere Zwischenschritte. Wähle wiederholt geeignete Dreiecke aus, in denen zwei Winkel bekannt sind, und berechne den dritten. So tastest du dich Schritt für Schritt an den eigentlich gesuchten Winkel heran.
Beispiel
Es soll der Winkel ε berechnet werden, wobei bekannt ist, dass w Winkelhalbierende von ∠BAC ist (siehe Abbildung).
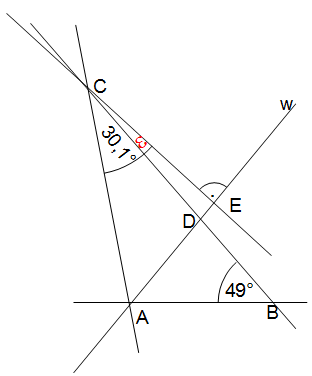
Bei einem beliebigen Vieleck mit n Ecken erhält man die Summe der Innenwinkel, indem man von der Eckenanzahl zwei abzieht und das Ergebnis mit 180° multipliziert:
- Viereck: 2 · 180°
- Fünfeck: 3 · 180°
- ...
- n-Eck: (n −2) · 180°

