Daten und Diagramme - Kenngrößen von Daten
Mittelwerte (Median, Modalwert, arithmetisches Mittel), Quartile, Maximum, Minimum, Spannweite; Erfassung von Daten in Boxplots, Interpretation von Boxplots

Statistische Kenngrößen, Median, Quartile, Boxplot
Statistische Kenngrößen:
Mittelwert / arithmetisches Mittel:
- Der Mittelwert ist die Summe aller Zahlen der Datenmenge geteilt durch die Anzahl der Zahlen in der Datenmenge.
Modalwert:
- Der Modalwert ist der Wert, der in der Datenmenge am häufigsten vorkommt.
Minimum:
- Das Minimum ist der kleinste Wert in der Datenmenge.
Maximum:
- Das Maximum ist der größte Wert in der Datenmenge.
Spannweite:
- Die Spannweite ist die Differenz von Maximum und Minimum.
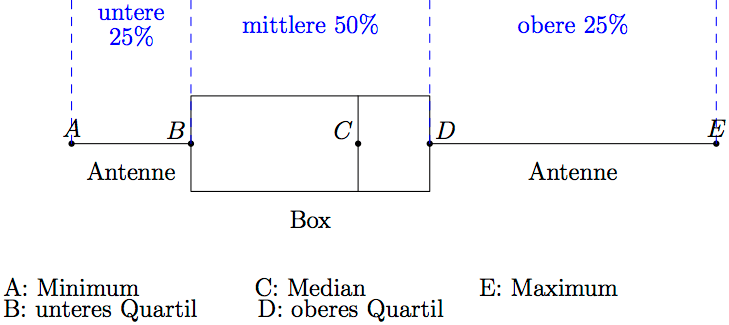
Ein Boxplot ist eine übersichtliche, graphische Veranschaulichung einer Datenmenge.
Um den Bereich der beiden Quartile zeichnet man eine Box. In dieser Box (oder auf ihrem Rand) liegen ungefähr 50% aller Daten. Innerhalb der Box ist der Median durch einen senkrechten Strich repräsentiert.
Unter dem unteren Quartil und über dem oberen Quartil liegen jeweils ungefähr 25% der Werte. Diese Bereiche werden durch die beiden "Antennen" von der Box aus bis zum Minimum bzw. Maximum markiert. Die Antennen veranschaulichen die Ausdehnung der gesamten Datenmenge.
 .
.
Verschiedene Mittelwerte:
Arithmetisches Mittel:
- Addiere alle Daten und dividiere die erhaltene Summe durch die Anzahl der Daten.
- Dies ist der gängigste Mittelwert.
- Beispiel: Notendurchschnitt berechnen.
Modalwert:
- Ermittle den Wert in der Datenmenge, der am häufigsten vorkommt.
- Beispiel: Ein Schuhgeschäft sollte die am häufigsten gebrauchte Schuhgröße (Modalwert) besonders oft vorrätig haben und nicht Schuhe in der mittleren (arithmetisches Mittel) Größe aller Menschen.
Statistische Kenngrößen:
Mittelwert / arithmetisches Mittel:
- Der Mittelwert ist die Summe aller Zahlen der Datenmenge geteilt durch die Anzahl der Zahlen in der Datenmenge.
Median (Zentralwert):
- In der geordneten Datenmenge der zentrale Wert (bei ungeradzahliger Datenreihe) bzw. das arithmetische Mittel der beiden zentralen Werte (geradzahlige Datenreihe).
Modalwert:
- Der Modalwert ist der Wert, der in der Datenmenge am häufigsten vorkommt.
Minimum:
- Das Minimum ist der kleinste Wert in der Datenmenge.
Maximum:
- Das Maximum ist der größte Wert in der Datenmenge.
Spannweite:
- Die Spannweite ist die Differenz von Maximum und Minimum.
|
| |||
|
| |||
|
| |||
|
| |||
|
| |||
|
| |||
|
|
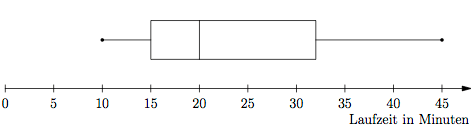
Ein Boxplot ist eine übersichtliche, graphische Veranschaulichung einer Datenmenge.
Der Boxplot zeigt sehr schnell, wie sehr und über welchen Bereich die Daten gestreut sind. Für die Erstellung eines Boxplots müssen die Daten zunächst der Größe nach geordnet werden. Dann werden 5 besondere Werte bestimmt:
- Minimum: kleinster Wert der Datenmenge
- Maximum: größter Wert der Datenmenge
- Median (Zentralwert): Der genau in der Mitte liegende Wert bzw. das arithmetische Mittel der beiden mittleren Werte (bei gerader Anzahl an Werten). Der Median teilt die Datenmenge in zwei Teile: Die Hälfte der Daten ist größer oder gleich dem Median, die andere Hälfte ist kleiner.
- Unteres Quartil: Median der ersten Datenhälfte (links vom Median)
- Oberes Quartil: Median der zweiten Datenhälfte (rechts vom Median)
Minimum: | ? |
unteres Quartil: | ? |
Median: | ? |
oberes Quartil: | ? |
Maximum: | ? |
Verschiedene Mittelwerte:
Arithmetisches Mittel:
- Addiere alle Daten und dividiere die erhaltene Summe durch die Anzahl der Daten.
- Dies ist der gängigste Mittelwert.
- Beispiel: Notendurchschnitt berechnen.
Median (Zentralwert):
- Sortiere alle Daten der Größe nach und ermittle dann den Wert in der Mitte der Liste. Am einfachsten streicht man dazu gleichzeitig den ersten und letzten, dann den zweiten und vorletzten, ... Wert der Liste durch, bis der mittlere Wert übrig bleibt.
- Bei einer geraden Anzahl von Daten bleiben zwei Werte in der Mitte übrig. Der Median ist in diesem Fall das arithmetische Mittel dieser beiden Zentralwerte.
- Der Median wird durch einen Ausreißer-Wert nicht beeinflusst, im Gegensatz zum arithmetischen Mittel. Darum wird er z.B. für die Ermittlung des Durchschnittseinkommens verwendet. Andernfalls würden wenige Superreiche das Bild verzerren.
Modalwert:
- Ermittle den Wert in der Datenmenge, der am häufigsten vorkommt.
- Beispiel: Ein Schuhgeschäft sollte die am häufigsten gebrauchte Schuhgröße (Modalwert) besonders oft vorrätig haben und nicht Schuhe in der mittleren (arithmetisches Mittel) Größe aller Menschen.
2 2 4 3 2 3
Arithmetisches Mittel: | ? |
Median: | ? |
Modalwert: | ? |

