Koordinatengeometrie im Raum - Geraden
Geradengleichung in Parameterform, parallele und senkrechte Geraden, Punkt auf Gerade, Spurpunkte, Verlauf durch Oktanten, besondere Lage zum Koordinatensystem, gegenseitige Lage von zwei Geraden
Um zu prüfen, ob der Punkt P auf der Geraden g liegt, setzt man die Koordinaten von P in die Gleichung von g (Parameterform) ein. Sofern sich der Parameter eindeutig bestimmen lässt, gilt P ∈ g.
Beispiel
| = |
|
Prüfe, ob die Punkte P(-1|3|5) und Q(3|-5|2) auf g liegen.
Um die Gerade g durch die Punkte A und B in Parameterform darzustellen, kann man z.B.
- A oder B als Aufpunkt und
- den Verbindungsvektor von A nach B als Richtungsvektor verwenden.
Beispiel
Gib die Gerade g = AB in Parameterform an mit A(1|-1|2) und B(-2|5|5).
Eine "besondere Lage zum Koordinatensystem" hat eine Gerade g z.B. dann, wenn
- sie durch den Ursprung geht und/oder
- sie parallel zu einer Koordinatenebene ist und/oder
- sie parallel zu einer Achse verläuft oder
- ihre Punkte zu zwei Achsen denselben Abstand haben oder
- ihre Punkte zu allen drei Achsen denselben Abstand haben.
Beispiel
Welche besondere Lage im Koordinatensystem haben folgende Geraden:
|
|
Um den evtl. Schnittpunkt (Spurpunkt) einer Geraden mit der x1x2-Ebene zu bestimmen, muss man innerhalb der Geradengleichung (Parameterform) x3 = 0 setzen.
Entsprechend setzt man x1 = 0, um den Schnittpunkt mit der x2x3-Ebene zu bestimmen und x2 = 0 für den Schnittpunkt mit der x1x3-Ebene.
Beispiel
| = |
|
Bestimme sämtliche Schnittpunkte mit den Koordinatenebenen.
Um zu ermitteln, durch welche Oktanten eine Gerade verläuft, sollten zunächst die Spurpunkte (Schnittpunkte mit den Koordinatenebenen) bestimmt werden.
Beispiel
Durch welche Oktanten verläuft die Gerade g:
?
X
| = |
|
Eine Geradengleichung lässt sich auch dann aufstellen, wenn keine festen Koordinaten vorgegeben sind. Alle weiteren Rechnungen erfolgen dann mit Hilfe der verwendeten Platzhalter (Buchstaben).
Beispiel
Gegeben ist eine Pyramide durch die Punkte A, B, C und S (siehe Skizze). D und E sind Seitenmitten.
- Bestimme für die Gerade DE eine Gleichung in Parameterform, wobei diese nur mit A, B, C und S ausgedrückt werden soll.
- Zeige, dass DE parallel zur Grundfläche der Pyramide verläuft.
Skizze: | 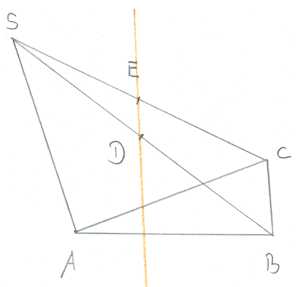 |

