Dreiecke - Kongruenz
Dreiecke daraufhin überprüfen, ob sie kongruent sind bzw. eindeutig definiert; eindeutige/mehrdeutige Konstruktion von Dreiecken aufgrund vorgegebener Größen
Lernvideo
Kongruenz von Dreiecken
Kanal: Mathegym
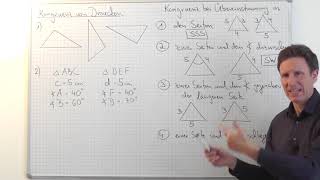
Die Kongruenz zweier Dreiecke erkennt man nicht immer sofort. Auf sein Augenmaß darf man sich außerdem auch nicht verlassen. Am sichersten lässt sich die Kongruenz zweier Dreiecke mit Hilfe der sog. Kongruenzsätze feststellen. Zwei Dreiecke sind demnach kongruent, wenn
- sie in allen drei Seiten übereinstimmen (SSS).
- sie in einer Seite und zwei zu dieser Seite gleich liegenden Winkeln übereinstimmen (WSW bzw. SWW).
- sie in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen (SWS).
- sie in zwei Seiten und dem Winkel, der der größeren Seite gegenüberliegt, übereinstimmen (SsW).
Zwei Figuren heißen kongruent, wenn sie deckungsgleich sind. Praktisch betrachtet heißt das, man kann sie so übereinander legen, dass an keiner Stelle etwas überlappt.

