Lineare Funktionen - Funktionsterm berechnen/interpretieren

Aus Gleichung Steigung und y-Achsen-Abschnitt herauslesen; Gleichung der Gerade durch zwei Punkte bzw. durch einen Punkt mit vorgegebener Steigung

Die Steigung m einer Geraden verrät durch ihr Vorzeichen, ob die Gerade steigt (m>0) oder fällt (m<0). Sonderfall: waagrechte Gerade (m=0). Am Betrag vom m sieht man, wie steil die Gerade verläuft. Je größer |m|, desto steiler die Gerade.

Liegt die Gerade als Zeichnung vor, kann man ihre Steigung m als Bruch angeben. Wähle dazu zwei beliebige Punkte auf der Geraden aus und zähle ab, wie viele Kästchen du vom linken Punkt aus nach rechts (⇒ Nenner von m) und von dort aus nach oben oder unten gehen musst (⇒ positiver bzw. negativer Zähler von m), um beim rechten Punkt anzukommen.

Beispiel
Bestimme die Steigung der Geraden.
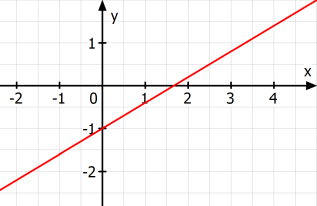
graphik
Ist eine Gerade g durch zwei Punkte A(x1|y1) und B(x2|y2) gegeben, so kann man ihre Steigung m so berechnen:
  1. Berechne die Differenz der y-Werte beider Punkte, also Δy = y2 − y1.
  2. Berechne ebenso die Differenz der x-Werte beider Punkte, also Δx = x2 − x1.
  3. Der Bruch Δy / Δx ergibt die Steigung m.
Beispiel
Ermittle die Steigung der Gerade, die durch die Punkte (-1,5 | 2,5) und (0 | -3) geht.
Folgende Ausnahmefälle hinsichtlich der Lage zweier Geraden sind zu beachten:
  • Beide Geraden sind (echt) parallel, haben also keinen Schnittpunkt. Das passiert, wenn beide Geraden dieselbe Steigung, aber unterschiedliche y-Achsenabschnitte haben. In dem Fall lässt sich die Gleichung g(x) = h(x) nicht lösen, es entsteht eine falsche Aussage wie z.B. 1=0.
  • Beide Geraden sind identisch, zu erkennen an derselben Steigung und demselben y-Achsenabschnitt. Die Gleichung g(x) = h(x) beschreibt in diesem Fall eine wahre Aussage wie z.B. 0 = 0, hat also unendlich viele Lösungen.
  • Eine Geraden ist senkrecht, z.B. x = 5; dann kann die andere Gerade sie, wenn überhaupt, nur bei x = 5 schneiden.
  • Eine Geraden ist waagrecht, z.B. y = 5; dann kann die andere Gerade sie, wenn überhaupt, nur in (?|5) schneiden.
Beispiel
f: y
=
1
8
 
x
+
2
     
g: x
=
4
     
h: y
=
3
     
i: y
=
0,125x
Untersuche paarweise, wie die Geraden zueinander liegen und bestimme gegebenenfalls den Schnittpunkt.
Sind zwei Geraden parallel, so besitzen sie dieselbe Steigung.

Sind zwei Geraden g und h zueiandner senkrecht (orthogonal), so erfüllen ihre Steigungen die Gleichung mg · mh = −1.

Mathe üben

Beispielaufgaben zum Selberrechnen

Wir haben für dich 24 Mathe-Aufgaben zum Thema Lineare Funktionen - Funktionsterm berechnen/interpretieren, die du bei uns online rechnen und lösen kannst.
Aufgaben rechnen