Tangentengleichung und Steigungswinkel
Bestimmung des Steigungswinkels einer Tangente/Normalen an einer vorgegebenen Stelle; Bestimmung der Tangente an einer vorgegebenen Stelle des Graphen bzw. mit vorgegebenen Eigenschaften (Steigung, Steigungswinkel); Bestimmung des Berührpunkts der Tangente, die durch einen bestimmten Punkt geht
Sei T: y = mx + t die Tangente an Gf im Punkt P[x0|f(0)]. Dann gilt:
m = f ´ (x0)
Beispiel 1
| = |
|
Bestimme die Tangente an Gf an der Stelle
x | = | 0,6. |
Beispiel 2
| = |
|
| geht. |
Beispiel 3
| = |
|
a) Bestimme die Tangente an Gf an der Stelle
x | = |
|
b) Bestimme alle Tangenten an Gf, die parallel sind zu
g: y | = |
|
Zu jeder Tangente T an Gf im Punkt P(x0|f(x0)) gibt es eine ebenfalls durch P gehende, zu T senkrechte Gerade N. Diese nennt man Normale. Sofern T nicht parallel zur x-Achse verläuft besteht zwischen den Steigungen von T und N folgender Zusammenhang:
mT·mN=−1
Sei T: y = mx + b die Tangente an Gf im Punkt P[x0|f(0)]. Dann gilt:
m = f ´ (x0)
Beispiel
| = |
|
a) Bestimme die Tangente an Gf an der Stelle
x | = |
|
b) Bestimme alle Tangenten an Gf, die parallel sind zu
g: y | = |
|
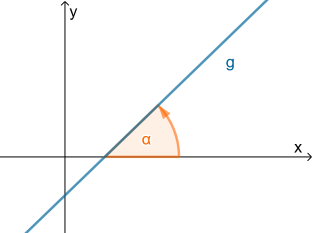
Der Steigungswinkel 0°≤α<180° einer Geraden bezeichnet die Größe des Winkels, um den g gegenüber der x-Achse gedreht ist. Für 0°<α<90° handelt es sich um eine steigende, für 90°<α<180° um eine fallende Gerade.
Die Steigung m einer Geraden und ihr Steigungswinkel α stehen in folgendem Zusammenhang:m=tan(α)
Beachte: wenn m gegeben und α gesucht ist, rechnet man zunächst tan-1(m) aus. Ist das Ergbnis positiv, hat man damit α ermittelt. Ist es negativ, addiert man noch 180° hinzu.
Beispiel
| = |
|
Berechne den Steigungswinkel der Tangente an
im Punkt P(0,5|?).
G | f |
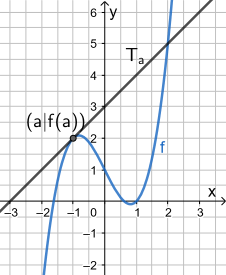
Die Schar aller Tangenten an einen Funktionsgraphen im Punkt (a|f(a)) kann durch eine Funktionsgeichung angegeben werden. Zur Ermittlung dieser Funktionsgleichung geht man genauso vor wie bei einer einzelnen Tangente. Der einzige Unterschied besteht darin, dass man mit allgemeinen Koordinaten a und f(a) rechnen muss statt mit festen Werten.
Beispiel
| = |
|
Bestimme die Gleichung für die Schar der Tangenten
an
im Punkt (a|f(a)).
T | a |
G | f |