Potenzfunktionen - natürlicher Exponent

Funktionen mit Funktionsterm a·xn; Bestimmung der Parameter

Potenzfunktionen vom Grad n
Lernvideo

Potenzfunktionen vom Grad n

Kanal: Mathegym
Bei einer Potenzfunktion mit der Funktionsgleichung y=axn entscheidet die Hochzahl n zusammen mit dem Vorfaktor a, von wo der Graph kommt und wohin er geht:
  • n ungerade, a positiv (z.B. 5x³): Graph verläuft von links unten nach rechts oben.
  • n ungerade, a negativ (z.B. -2x): Graph verläuft von links oben nach rechts unten.
  • n gerade, a positiv (z.B. ½x²): Graph verläuft von links oben nach rechts oben.
  • n gerade, a negativ (z.B. -x²): Graph verläuft von links unten nach rechts unten.
Beispiel
Wie verläuft der Graph?
y
=
4x
7
Potenzfunktionen sind Funktionen der Form:
y = axn

Spezialfälle:
  • n = 0 (konstante Funktion): y = a, Graph: waagerechte Gerade
  • n = 1 (lineare Funktion): y = ax, Graph: Ursprungsgerade mit Steigung a
  • n = 2 (quadratische Funktion): y = ax2, Graph: gestauchte / gestreckte Parabel mit Scheitel S ( 0 | 0 )
Die Graphen von Potenzfunktionen haben charakteristische Eigenschaften, die oft davon abhängen, ob die Hochzahl n gerade oder ungerade ist.
  • Wertemenge:
    n gerade: keine negativen Zahlen
    n ungerade: alle reellen Zahlen

  • Symmetrie:
    n gerade: Achsensymmetrie zur y-Achse
    n ungerade: Punktsymmetrie zum Ursprung

  • Vorfaktor a
    Der Wert des Parameters a ist der Funktionswert an der Stelle x = 1.
    a>0: Streckung / Stauchung in y-Richtung
    a<0: zusätzliche Spiegelung an der x-Achse
Beispiel
Gib die zugehörige Funktionsgleichung an
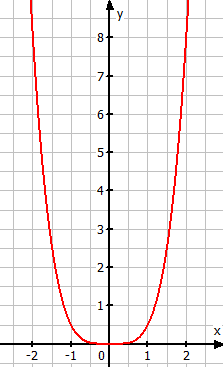
graphik
y
=
?x
?
Beispiel
Das erste Beispiel in folgendem Video zeigt, wie man die Funktionsgleichung einer Potenzfunktion durch zwei Punkte ermittelt, wenn einer der beiden Punkte die x-Koordinate 1 hat.
Wenn von einem Punkt auf dem Schaubild nur die x-Koordinate bekannt ist, erhält man die y-Koordinate, indem man die x-Koordinate in den Funktionsterm einsetzt und den Wert des Funktionsterms berechnet. Das Ergebnis ist die y-Koordinate.

Wenn von einem Punkt auf dem Schaubild nur die y-Koordinate bekannt ist, erhält man die x-Koordinate, indem man den Funktionsterm gleich der y-Koordinate setzt und aus der entstehenden Gleichung x bestimmt. Das Ergebnis ist die x-Koordinate.
Die Graphen-Schnittpunkte zweier Potenzfunktionen der Art a·xn erhält man, indem man der Reihe nach...
  1. (wie üblich) die beiden Funktionsterme zunächst gleichsetzt,
  2. mit der linken Seite subtrahiert, so dass eine "...=0"-Gleichung entsteht,
  3. auf der linken Seite die kleinere der beiden x-Potenzen ausklammert,
  4. die beiden Faktoren (x-Potenz und Klammer dahinter) nacheinander gleich null setzt.
Bemerkung: Beide Graphen schneiden sich immer im Ursprung des Koordinatensystems. Ob es weitere Schnittpunkte gibt und wie viele, erkennt man, indem man die Graphen skizziert. Beachte beim Lösen auch die symmetrischen Eigenschaften der Graphen, damit sparst du dir Rechenarbeit.
Beispiel
f
 
x
=
1
3
 
x
7
g
 
x
=
3
 
x
5
Ermittle die Anzahl der Schnittpunkte beider Graphen durch grobe Skizze und bestimme die genauen Koordinaten rechnerisch.
Mathe üben

Beispielaufgaben zum Selberrechnen

Wir haben für dich 46 Mathe-Aufgaben zum Thema Potenzfunktionen - natürlicher Exponent, die du bei uns online rechnen und lösen kannst.
Aufgaben rechnen