Parabel › Mathe-Aufgaben online
Online-Übungen zum Thema "Parabel", die du direkt im Browser bearbeiten und lösen kannst. Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

-
≈9. Klasse - Aufgaben + Stoff + Video
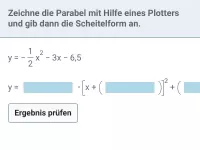
Quadratische Funktionen - Darstellungsformen
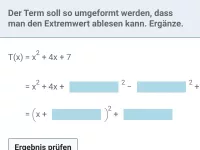
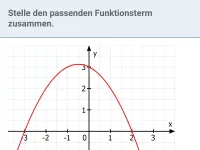
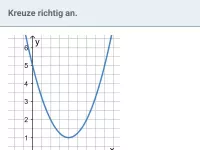
Allgemeine Form (Normalform) - Scheitelpunktform - Nullstenform (Produktform); aus Graph ablesen und Umwandlung, u.a. mit quadratischer Ergänzung -
≈9. Klasse - Aufgaben + Stoff + Video
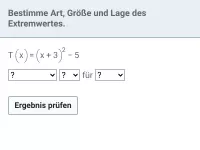
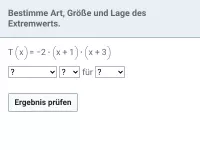
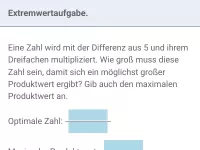
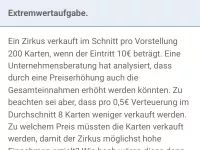
Quadratische Funktionen - Extremwertaufgaben
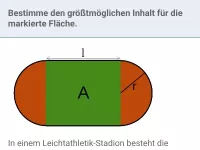
Minimum und Maximum anhand von Grafiken ablesen können, Extremwertaufgaben/Optimierungsaufgaben im Sachzusammenhang -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratische Funktionen - Parameter mittels Gleichungssystem bestimmen
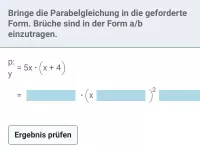
Durch vorgegebene Punkte oder anhand der gezeichneten Parabel sind a, b und c mittels Geichungssystem zu bestimmen. -
≈9. Klasse - Aufgaben + Stoff + Video
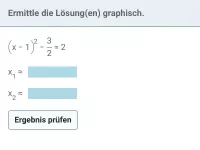
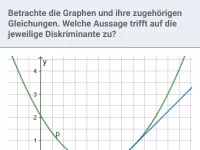
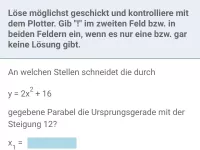
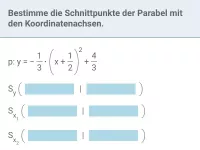
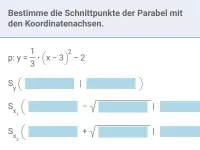
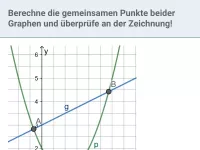
Quadratische Gleichungen - Schnittprobleme
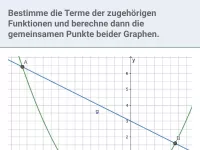
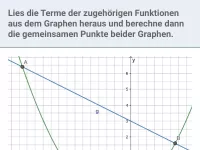
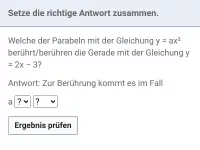
Graphische Interpretation quadratischer Gleichungen; Bestimmung der Schnittpunkte von Parabeln bzw. Parabel und Gerade; Parameterbestimmung in Abhängigkeit von der Anzahl gemeinsamer Punkte
Fragen und Antworten zum Thema "Parabel"
- Bei einer Parabelgleichung lassen sich mehrere Formen unterscheiden. Benenne diese und gib die jeweilige Termstruktur an. Wie lässt sich von der einen Form in die andere umwandeln?
- Wie ermittelt man die Schnitt- bzw. Berührpunkte zweier Graphen? Welchen Spezialfall kann man dabei betrachten?
- Wie kann man, wenn f und g Funktionen sind, die Gleichungen f(x) = h(x) bzw. f(x) = 0 graphisch interpretieren? Was gilt für den Spezialfall, dass es sich um eine quadratische Gleichung handelt?
- Wie ermittelt man die Funktionsgleichung einer Parabel, die durch drei Punkte gegeben ist?
- Wie lässt sich jede Gleichung graphisch lösen (falls lösbar)?
- Wie ist die Gleichung einer Parabel y = ax² + bx + c (allgemeine Form) mit dem Scheitel S(s ; t) in Scheitelform anzugeben?
- Wie kann man den Scheitel einer Parabel bestimmen, wenn man ihre Schnittstellen mit der x-Achse kennt?
- Wie geht man vor, um herauszufinden, ob - und wenn ja: wo - eine Parabel und eine Gerade bzw. zwei Parabeln sich schneiden/berühren?
- Beschreibe das Vorgehen bei Extremwertaufgaben (vier Schritte).
- Wie bestimmt man die allgemeine Funktionsgleichung y=ax²+bx+c einer quadratischen Funktion, wenn man einen der Parameter kennt und der Graph vorliegt?
- Wie geht man vor, um herauszufinden, ob - und wenn ja: wo - eine Parabel und eine Gerade bzw. zwei Parabeln sich schneiden/berühren?
- Wie kommt man von der Scheitelpunktform zur allgemeinen Form der Gleichung einer Parabel?
- Nenne und beschreibe die drei Darstellungsformen quadratischer Funktionen.
- Beschreibe, wie man von jeder einzelnen Darstellungsform aus in die beiden anderen Formen umwandelt.
- Wie kann man Parabeln in Sachzusammenhängen modellieren? Gib in Abhängigkeit der gegebenen Punkte an, wie man jeweils vorgehen sollte.
- Wie viele Nullstellen kann eine quadratische Funktion maximal haben und wie findet man sie?
- Eine Funktion habe als Graph eine nach unten bzw. nach oben geöffnete Parabel. Wo hat die Funktion ein Maximum bzw. Minimum und wie groß ist dieses? Wann ergibt sich ein Maximum und wann ein Minimum?