07.2.1 Potenzfunktion - rationaler Exponent - Definitionsmenge, Umkehrfunktionen - Matheaufgaben

Definitionsmenge, Graph und Umkehrfunktion von Potenzfunktionen mit rationalem Exponent - Lehrplan Baden-Württemberg, berufliches Gymnasium, 11. Klasse/12. Klasse

Du bist nicht angemeldet!
Hast du bereits ein Benutzer­konto? Dann logge dich ein, bevor du mit Üben beginnst.
Login
Hilfe
  • Allgemeine Hilfe zu diesem Level
    Eine Funktion mit der Gleichung y = xr, r∈ℚ, heißt Potenzfunktion. Ihre maximale Definitionsmenge hängt vom Exponenten r ab.
    • Ist r negativ, so lässt sich die Potenz in einen Bruch umwandeln und damit scheidet "x=0" aus (denn der Nenner darf nicht Null sein).
    • Ist r= p/q ein Bruch und keine ganze Zahl, so lässt sich die Potenz in eine Wurzel umwandeln und damit scheidet "x<0" aus (denn die Wurzel einer negativen Zahl ist nicht definiert).

Bestimme die maximale Definitionsmenge.

f(x)
=
x
1
3
 ; D=
ℝ
ℝ
+
ℝ
+
0
ℝ\{0}
  • Nebenrechnung
Checkos: 0 max.
Eine Funktion mit der Gleichung y = xr, r∈ℚ, heißt Potenzfunktion. Ihre maximale Definitionsmenge hängt vom Exponenten r ab.
  • Ist r negativ, so lässt sich die Potenz in einen Bruch umwandeln und damit scheidet "x=0" aus (denn der Nenner darf nicht Null sein).
  • Ist r= p/q ein Bruch und keine ganze Zahl, so lässt sich die Potenz in eine Wurzel umwandeln und damit scheidet "x<0" aus (denn die Wurzel einer negativen Zahl ist nicht definiert).
Ist eine Funktion umkehrbar, so erhält man den Term der Umkehrfunktion nach folgendem Rezept:
  1. Löse die Gleichung y = f(x) nach x auf.
  2. Vertausche dann x und y.
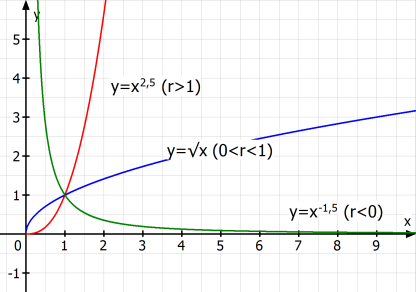
Potenzfunktionen f mit dem Funktionsterm f(x) = xr, r∈ℚ, können graphisch ganz unterschiedlich aussehen. Grob lassen sich drei Klassen unterscheiden:
  • r<0: der Graph ähnelt der Hyperbel mit der Gleichung y=1/x. Prägnante Erkennungsmerkmale: die Koordinatenachsen als Asymptoten. Je größer |r| (also der Betrag von r), desto schneller nähert sich der Graph der x-Achse an. Ansonsten ist zu unterscheiden, ob r eine ganze Zahl ist oder nicht. Falls nicht, so ist der Graph nur rechts von der y-Achse definiert. Andernfalls ist die Hyperbel symmetrisch zur y-Achse (r gerade) bzw. zum Ursprung (r ungerade).
  • 0<r<1: ähnlich dem Graph der Wurzelfunktion y = √x. Prägnante Erkennungsmerkmale: nur für x≥0 definiert, streng monoton steigend, für große x ins Unendliche wachsend, aber mit nachlassender Steigung. Je größer |r|, desto schneller geht der Graph für große x-Werte nach oben.
  • r>1: ähnlich der Normalparabel y=x², allerdings nur für x≥0 definiert - es sei denn, r ist eine natürliche Zahl: in diesem Fall symmetrisch zur y-Achse, falls r gerade bzw. zum Ursprung, falls r ungerade. Auch hier gilt: Je größer |r|, desto schneller geht der Graph für große x-Werte nach oben.