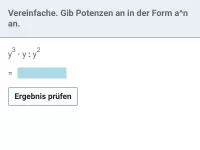
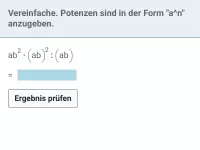
Ein Term wie z.B. a · a³ : a² kann einfacher geschrieben werden. Wie?

Produkte und Quotienten von Variablen(-Potenzen) lassen sich, sofern die Variable immer dieselbe ist, zu einer Potenz zusammenfassen. Z.B.
a · a3 : a2 = a4 : a2 = a2
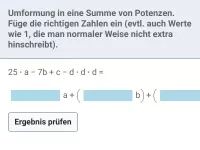
Beispiel 1
Schreibe als Summe von Variablenpotenzen mit passendem Vorfaktor:
5
·
x
·
x
·
x
−
y
=
?
3
·
c
−
a
·
a
·
a
·
a
·
a
+
b
·
b
:
2
=
?
Lösung:
5
·
x
·
x
·
x
−
y
=
5x
3
+
−
1y
1
- - - - - - - - - -
3
·
c
−
a
·
a
·
a
·
a
·
a
+
b
·
b
:
2
=
3c
+
−
1a
5
+
1
2
 
b
2
=
−
1a
5
+
1
2
 
b
2
+
3c
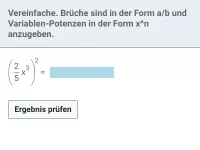
Beispiel 2
Fasse zusammen:
a
3
·
a
2
:
a
6
Lösung:
a
3
·
a
2
a
6
=
a
·
a
·
a
·
a
·
a
a
·
a
·
a
·
a
·
a
·
a
=
a
·
a
·
a
·
a
·
a
a
·
a
·
a
·
a
·
a
·
a
kürzen
=
a
·
a
·
a
·
a
a
·
a
·
a
·
a
·
a
=
a
·
a
·
a
·
a
a
·
a
·
a
·
a
·
a
weiter kürzen
=
1
a
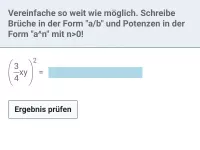
Beispiel 3
Fasse zusammen:
xy
3
:
x
2
·
y
2
xy
3
:
x
2
·
y
2
=
xy
·
xy
·
xy
:
x
2
·
y
2
=
x
·
x
·
x
:
x
2
·
y
·
y
·
y
·
y
2
=
x
·
y
5
Erläuterung: in der dritten Zeile wurden die Faktoren (bzw. Quotienten) nach x und y sortiert, um dann in der letzten Zeile leichter zusammenfassen zu können.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen