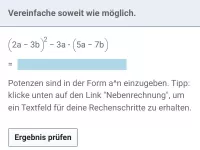
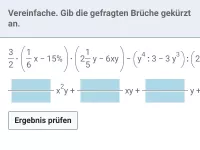
Zwei eingeklammerte Terme, in denen jeweils nur Plusrechnung vorkommt, werden miteinander multipliziert. Wie löst man die Klammern auf?

Beim Multiplizieren zweier Summen muss jeder Summand der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert werden (ergibt sich aus dem Distributivgesetz):

(a + b) · (c + d) = ac + ad + bc + bd

Beispiel 1
Multipliziere aus und vereinfache:
2
5
 
uv
−
2
3
·
15u
2
+
1
−
uv
- - - - - - - - - - - - - - - - - Tipp: Klammern vorher in Summen umwandeln:
2
5
 
uv
 
+
 
−
2
3
·
15u
2
 
+
 
1
 
+
 
−
uv
=
- - - - - - - - - - - - - - - - - "jeder mit jedem":
2
5
 
uv
·
15u
2
6u
3
v
+
2
5
 
uv
·
1
2
5
 
uv
+
2
5
 
uv
·
−
uv
−
2
5
 
u
2
v
2
+
−
2
3
·
15u
2
−
10u
2
+
−
2
3
·
1
−
2
3
+
−
2
3
·
−
uv
2
3
 
uv
=
- - - - - - - - - - - - - - - - - Zusammenfassen gleichartiger Terme:
6u
3
v
+
6
15
 
uv
+
10
15
 
uv
−
2
5
 
u
2
v
2
−
10u
2
−
2
3
=
6u
3
v
+
1
1
15
 
uv
−
2
5
 
u
2
v
2
−
10u
2
−
2
3
Beispiel 2
b
−
2
3
 
b
·
6a
·
a
−
30%
+
1
2
 
a
2
·
b
−
4ab
−
ab
2
Lösung siehe Video:
Distributivgesetz, Termvereinfachung, Beispiel 2
Lernvideo

Distributivgesetz, Termvereinfachung, Beispiel 2

Kanal: Mathegym
Beispiel 3
Multipliziere aus und vereinfache:
a) 
x
+
3
·
4
−
5x
b) 
−
10
−
a
·
−
7
+
b
c) 
x
2
−
1
−
2
3
 
a
·
3x
−
1
2
a)
x
+
3
·
4
−
5x
=
x
·
4
4x
+
x
·
−
5x
−
5x
2
+
3
·
4
12
+
3
·
−
5x
−
15x
=
4x
−
15x
−
11x
−
5x
2
+
12
=
−
11x
−
5x
2
+
12
b)
−
10
−
a
·
−
7
+
b
=
−
10
·
−
7
70
·
−
10
·
b
−
10b
+
−
a
·
−
7
7a
+
−
a
·
b
−
ab
=
70
−
10b
+
7a
−
ab
c)
x
2
−
1
−
2
3
 
a
·
3x
−
1
2
=
x
2
·
3x
3x
3
+
x
2
·
−
1
2
−
1
2
 
x
2
+
−
1
·
3x
−
3x
+
−
1
·
−
1
2
1
2
+
−
2
3
 
a
·
3x
−
2ax
+
−
2
3
 
a
·
−
1
2
1
3
 
a
=
3x
3
−
1
2
 
x
2
−
3x
+
1
2
−
2ax
+
1
3
 
a
2 KLAMMERN ausmultiplizieren – Klammer mal Klammer auflösen mit x, Terme vereinfachen
Lernvideo

2 KLAMMERN ausmultiplizieren – Klammer mal Klammer auflösen mit x, Terme vereinfachen

Kanal: MathemaTrick
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen