Gib die allgemeine Gleichung für eine lineare Funktion an und erkläre die Bedeutung der Parameter m und t.
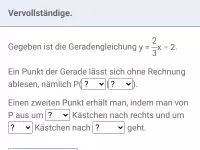
Eine lineare Funktion mit der Gleichung y = m·x + t ergibt graphisch immer eine Gerade. Dabei ist m die Steigung (zeigt an, wie stark die Gerade steigt oder fällt) und t der y-Achsenabschnitt (zeigt an, wo die Gerade die y-Achse schneidet) der Gerade.
- Ist m positiv, so steigt die Gerade (von links nach rechts)
- Ist m negativ, so fällt die Gerade (von links nach rechts)
- Ist m = 0, so verläuft die Gerade parallel zur x-Achse
Beispiel
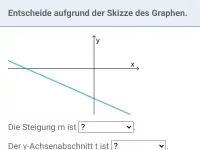
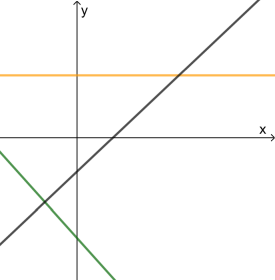
Welche Informationen lassen sich bzgl. der Steigung m und des y-Achsenabschnitts t ablesen?
Lösung:
- Schwarz: die Gerade steigt, d.h. m > 0 und schneidet die y-Achse im negativen Bereich, d.h. t < 0
- Grün: die Gerade fällt, d.h. m < 0 und schneidet die y-Achse im negativen Bereich, d.h. t < 0
- Orange: die Gerade ist parallel zur x-Achse, d.h. m = 0 und schneidet die y-Achse im positiven Bereich, d.h. t > 0
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈8. Klasse - Aufgaben + Stoff + Video
Lineare Funktionen - Ablesen am Graphen
Graphische Darstellung linearer Funktionen (Steigung und y-Achsenabschnitt), zeichnerische Schnittpunktbestimmung, graphisches Lösen von linearen Gleichungen, Textaufgaben -
≈8. Klasse - Aufgaben + Stoff + Video
Lineare Funktionen - Funktionsterm berechnen/interpretieren
Aus Gleichung Steigung und y-Achsen-Abschnitt herauslesen; Gleichung der Gerade durch zwei Punkte bzw. durch einen Punkt mit vorgegebener Steigung
Ähnliche Themen
- Von einer Geraden kennst du die Steigung sowie einen Punkt. Wie lässt sich daraus der y-Achsenabschnitt berechnen?
- Wie berechnet man die Steigung einer Geraden, wenn man zwei Punkte kennt, die auf ihr liegen?
- Durch welche Gleichungen werden senkrechte bzw. waagrechte Geraden beschrieben?
- Wie ermittelt man die Gleichung einer Geraden, wenn zwei Punkte gegeben sind?
- Welche drei Ausnahmefälle sind zu beachten, wenn man die Lage zweier Geraden zueinander untersucht?
- Wie kann man eine lineare Gleichung zeichnerisch lösen?
- Wie lässt sich eine lineare Gleichung, die zwei Variablen enthält, interpretieren?
- Was lässt sich über die Steigungen zweier Geraden sagen, die parallel bzw. senkrecht zueinander liegen?
- Von einer Geraden kennst du den Schnittpunkt mit der y-Achse sowie einen weiteren Punkt. Wie lässt sich daraus die Steigung rechnerisch bestimmen?
- Wie lässt sich eine Gerade g zeichnen, wenn man die Steigung m und den y-Achsenabschnitt t kennt?
- Wie lässt sich der Funktionsterm einer abgebildeten Gerade ermitteln?
- Wie ermittelt man die Steigung einer Geraden?
- Wie kann man aus den Steigungen und den y-Abschnitten zweier Geraden ohne Rechnung ihre gegenseitige Lage ermitteln?
- Erkläre, wie du rechnerisch prüfen kannst, dass drei gegebene Punkte auf einer Geraden liegen.