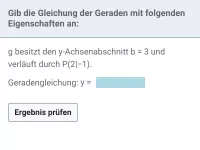
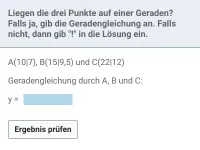
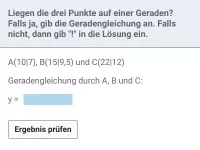
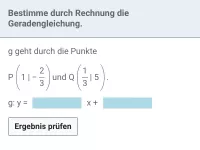
Wie ermittelt man die Gleichung einer Geraden, wenn zwei Punkte gegeben sind?
Ist eine Gerade durch zwei Punkte gegeben, so geht man wie folgt vor, um ihre Gleichung, sprich m und t, zu ermitteln:
- Bestimme zunächst die Steigung m = Δy / Δx .
- Setze dann in die Gleichung y = m·x + t einen der beiden Punkte ein und löse die Gleichung nach t auf.
Beispiel
Ermittle die Gleichung der Geraden g, die durch die Punkte P1(−3|2) und P2(5|−4) geht.
- Ermittlung von m
| = |
|
| = | 8 |
| = |
|
- Ermittlung von t
Setze
sowie einen der beiden Punkt, z.B.
in die allgemeine Geradengleichung
ein und löse nach t auf.
m | = |
|
P | 1 |
y | = |
|
| = |
| m einsetzen | |||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
| ||||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
| ||||||||||||||||||
Die Gleichung der Geraden g lautet damit
.
|
Lernvideo
Gerade durch zwei Punkte (lineare Funktion)
Kanal: Mathegym
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈8. Klasse - Aufgaben + Stoff + Video
Lineare Funktionen - Funktionsterm berechnen/interpretieren
Aus Gleichung Steigung und y-Achsen-Abschnitt herauslesen; Gleichung der Gerade durch zwei Punkte bzw. durch einen Punkt mit vorgegebener Steigung1. Level6 Aufgaben
2. Level6 Aufgaben
3. Level6 Aufgaben
4. Level6 Aufgaben
5. Level6 Aufgaben
6. Level6 Aufgaben
7. Level6 Aufgaben
8. Level6 Aufgaben
9. Level6 Aufgaben
10. Level5 Aufgaben
11. Level5 Aufgaben
12. Level5 Aufgaben
13. Level5 Aufgaben
14. Level6 Aufgaben
15. Level3 Aufgaben
16. Level3 Aufgaben
17. Level5 Aufgaben
18. Level5 Aufgaben
19. Level5 Aufgaben
20. Level3 Aufgaben
21. Level5 Aufgaben
22. Level5 Aufgaben
23. Level5 Aufgaben
Ähnliche Themen
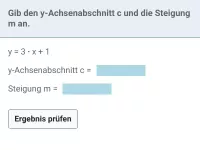
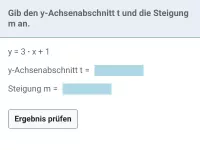
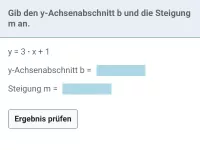
- Gib die allgemeine Gleichung für eine lineare Funktion an und erkläre die Bedeutung der Parameter m und t.
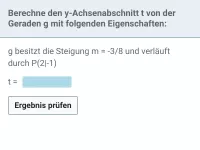
- Von einer Geraden kennst du die Steigung sowie einen Punkt. Wie lässt sich daraus der y-Achsenabschnitt berechnen?
- Wie berechnet man die Steigung einer Geraden, wenn man zwei Punkte kennt, die auf ihr liegen?
- Welche drei Ausnahmefälle sind zu beachten, wenn man die Lage zweier Geraden zueinander untersucht?
- Was lässt sich über die Steigungen zweier Geraden sagen, die parallel bzw. senkrecht zueinander liegen?
- Gib den allgemeinen Funktionsterm einer Geraden an und erkläre die Bedeutung der darin vorkommenden Parameter.
- Wie ermittelt man die Gleichung einer Geraden, wenn zwei Punkte gegeben sind?
- Gib die allgemeine Gleichung einer Geraden an und erkläre, was die darin vorkommenden Parameter bedeuten.
- Wie kann bei einer Geraden mit bekannter Steigung aus einem gegebenen Punkt der Achsenabschnitt ausgerechnet werden?
- Wie ermittelt man die Gleichung einer Geraden, wenn zwei Punkte gegeben sind?
- Wie wird bei einer Geraden mit bekannten y-Achsenabschnitt aus einem gegebenen Punkt die Steigung berechnet?
- Von einer Geraden kennst du den Schnittpunkt mit der y-Achse sowie einen weiteren Punkt. Wie lässt sich daraus die Steigung rechnerisch bestimmen?
- Wie ermittelt man die Steigung einer Geraden?
- Wie kann man aus den Steigungen und den y-Abschnitten zweier Geraden ohne Rechnung ihre gegenseitige Lage ermitteln?
- Erkläre, wie du rechnerisch prüfen kannst, dass drei gegebene Punkte auf einer Geraden liegen.
- Erkläre, wie du rechnerisch prüfen kannst, dass drei gegebene Punkte auf einer Geraden liegen.