Was ist bei der Multiplikation und Division von Quadratwurzeln möglich und welcher Zusammenhang besteht zum teilweisen Radizieren?

Ein Produkt von Wurzeln lässt sich als Produkt unter einer Wurzel schreiben und umgekehrt. Sofern weder a noch b negativ sind, gilt also

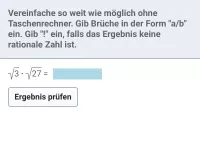
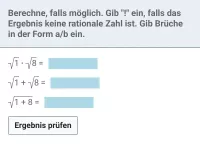
√a · √b = √(a · b)

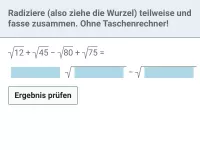
Unter anderem ermöglicht diese Regel, Wurzeln teilweise zu radizieren. Sofern a nicht negativ ist, kann man den Faktor a² unabhängig vom Faktor b radizieren:

√(a² · b) = √(a²) · √b = a · √b

Beispiel 1
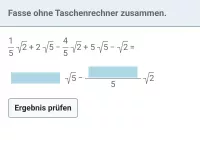
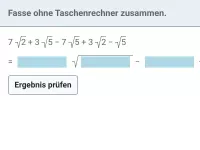
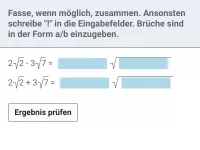
Vereinfache:
3
 
45
·
18
=
?
- - - - - - - - - - - - - - - - unter eine Wurzel fassen
3
 
45
·
18
=
- - - - - - - - - - - - - - - - teilweise radizieren
3
 
5
·
9
·
9
·
2
=
3
 
9
2
·
10
=
3
·
9
 
10
=
27
 
10
Beispiel 2
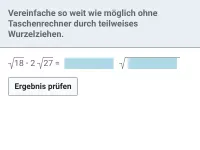
Radiziere teilweise:
720
=
?
- - - - - - - - - - - - - Zerlege den Radikand in möglichst quadratische Faktoren:
10
·
72
=
10
·
2
·
36
=
5
·
2
·
2
·
36
=
5
·
4
·
36
=
- - - - - - - - - - - - - 4 radizieren:
2
 
5
·
36
;
2
 
5
·
36
=
- - - - - - - - - - - - - 36 radizieren:
2
·
6
 
5
=
12
 
5
Weitere Beispiele (auch Brüche) siehe Video
:
Teilweise WURZELZIEHEN mit Brüchen – Teilweises Radizieren
Lernvideo

Teilweise WURZELZIEHEN mit Brüchen – Teilweises Radizieren

Kanal: MathemaTrick
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen