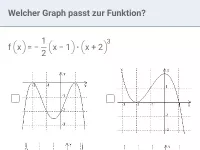
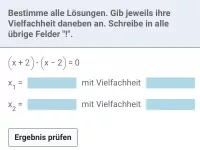
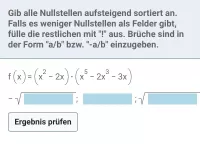
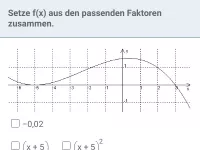
Was besagt die Vielfachheit einer Nullstelle?

Jede Nullstelle einer ganzrationalen Funktion besitzt eine bestimmte Vielfachheit.

Ist a eine Nullstelle, so kann f(x) als Produkt mit Faktor x − a geschrieben werden. Kommt x − a genau n mal als Faktor vor (also "hoch n"), so nennt man a eine n-fache Nullstelle.

Beispiel
Bestimme jeweils die Nullstellen und ihre Vielfachheiten:
f(x)
=
x
−
1
2
·
x
+
2
g(x)
=
x
2
+
1
·
x
2
−
4
h(x)
=
x
−
5
2
+
2
Lösung:
  • zu f
f besitzt die doppelte Nullstelle x = 1 und die einfache Nullstelle x = −2. Dies hat damit zu tun, dass der Faktor x − 1 doppelt ("hoch 2"), der Faktor x + 2 nur einfach vorkommt.
  • zu g
Vorsicht: Die erste Klammer liefert keine Nullstelle (Wert immer positiv durch das Quadrat + 1), die zweite wiederum kann mit der 3. binomischen Formel zerlegt werden und liefert damit die jeweils einfachen Nullstellen −2 und 2.
g(x)
=
x
2
+
1
·
x
+
2
·
x
−
2
  • zu h
Vorsicht: Im Gegensatz zu den vorhergehenden Beispielen ist der (potenzierte) Klammerterm kein Produkt, sondern ein Summand; damit ist 5 auch keine Nullstelle; bei näherer Betrachtung stellt man fest, dass h keine Nullstelle besitzt, da durch das "Quadrat + 2" der Funktionsterm immer positiv ist.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen