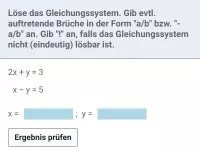
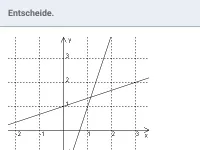
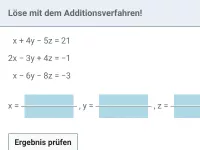
Welche Verfahren zum Lösen von Gleichungssystemen gibt es und worauf laufen diese stets hinaus?

Gleichungssysteme lassen sich z.B. mit Hilfe des Einsetzungsverfahrens oder des Additionsverfahrens lösen. Beide Verfahren laufen darauf hinaus, Gleichungen mit jeweils nur einer Unbekannten zu erhalten, nach der man dann auflösen kann.
Beispiel 1

Löse mit Hilfe des Einsetzungsverfahrens:

I: 2x + 3y = 5
II: 3y − x = 0,5

Lösung: Löse (II) nach x auf und setze das Ergebnis in (I) für x ein. Dadurch fällt die Variable x weg.

II:   
 
x
=
3y
−
0,5
in I:   
 
2
·
3y
−
0,5
+
3y
=
5
6y
−
1
+
3y
=
5
9y
−
1
=
5
+
1
9y
=
6
:
9
y
=
2
3
in II:   
 
x
=
3
·
2
3
−
0,5
x
=
1,5
Lineare Gleichungssysteme, Einsetzverfahren, Beispiel
Lernvideo

Lineare Gleichungssysteme, Einsetzverfahren, Beispiel

Kanal: Mathegym
Gleichungssysteme lösen Einsetzungsverfahren – LGS lösen 2 Unbekannte
Lernvideo

Gleichungssysteme lösen Einsetzungsverfahren – LGS lösen 2 Unbekannte

Kanal: MathemaTrick
Beispiel 2

Löse mit Hilfe des Additionsverfahrens:

I: 2x + 3y = 5
II: 3y − x = 0,5

Lösung: Die Variable x fällt heraus, wenn man zu (I) das Doppelte von (II) addiert:

I:    2x + 3y = 5
2·II:    − 2x + 6y =1
I + 2·II:    9y = 6

Jetzt geht es weiter wie beim Einsetzverfahren (siehe vorausgehendes Beispiel).
 
Lernvideo

Kanal:
Video-ID "zaT9nz4a2ZQ" existiert nicht
Beispiel 3
Löse mit Hilfe des Additionsverfahrens:
2x
+
3y
=
5
2y
−
3
=
x
Lösung siehe Video:
Lineare Gleichungssysteme, Additionsverfahren, Beispiel 2
Lernvideo

Lineare Gleichungssysteme, Additionsverfahren, Beispiel 2

Kanal: Mathegym
ADDITIONSVERFAHREN mit 2 Variablen – lineare Gleichungssysteme lösen
Lernvideo

ADDITIONSVERFAHREN mit 2 Variablen – lineare Gleichungssysteme lösen

Kanal: MathemaTrick
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen