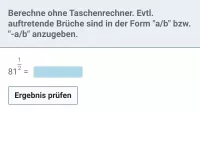
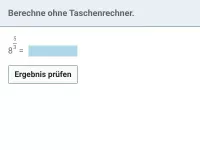
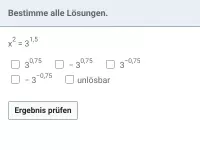
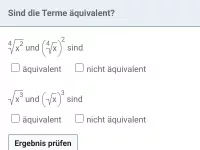
Sei T(x) ein beliebiger Term und r eine rationale Zahl. Wie lässt sich die Gleichung T(x)r = a lösen bzw. in welchen Fällen gibt es keine Lösung?

Sei T(x) ein beliebiger Term und r eine rationale Zahl. Die Gleichung

T(x)r = a

lässt sich (evtl.) lösen, indem man beide Seiten zunächst mit "1/r" potenziert. Dadurch erhält man:

T(x) = a1/r

Keine Lösung erhält man z.B., wenn a negativ und r
  • eine gerade Zahl ist: x² = -1 (x² nie negativ)
  • eine echt rationale Zahl ist: x1/3 = -1 (Ergebnis eines Wurzelterms nie negativ)
Beispiel
Löse die folgenden beiden Gleichungen:
1
3
 
x
+
1
−
3
4
=
8
 
          
 
3
x
2
−
2
=
−
1
2
Lösung:
1
3
 
x
+
1
−
3
4
=
8
"hoch -4/3"
1
3
 
x
+
1
=
8
−
4
3
1
3
 
x
+
1
=
1
8
4
3
1
3
 
x
+
1
=
3
1
8
4
1
3
 
x
+
1
=
1
2
4
1
3
 
x
+
1
=
1
16
−
1
1
3
 
x
=
−
15
16
·
3
x
=
−
45
16
- - - - - - - - - - - - -
3
x
2
−
2
=
−
1
2
Diese Gleichung ist unlösbar, weil das Ergebnis der Wurzel nicht negativ sein kann.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen