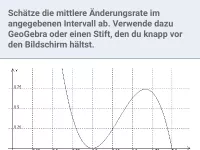
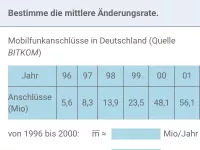
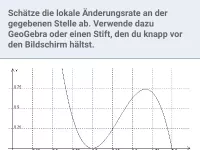
Wie bestimmt man die mittlere Änderungsrate einer Funktion? Welcher synonyme Begriff ist gebräuchlich?

Die mittlere Änderungsrate einer Funktion f im Intervall [a; b] ergibt sich durch

[ f(b) − f(a) ] / ( b − a)

Aufgrund seiner Struktur nennt man diesen Term auch Differenzenquotient.
Beispiel
(1) Maximilian war Ende Januar 1,35 m groß und Ende Juni 1,37 m. Wie groß ist in diesem Zeitraum die durchschnittliche Änderungsrate?
(2) Wie groß ist die durchschnittliche Änderungsrate der Normalparabel mit Scheitel im Ursprung im Intervall [3;7]?
  • Maximilian
Mit "1" ist der Januar, mit "6" der Juni gemeint:
137
−
135
6
−
1
=
2
5
=
0,4
 
cm/Monat
Also
 
4 mm pro Monat
  • Normalparabel
f
 
7
−
f
 
3
7
−
3
=
7
2
−
3
2
4
=
10
Interpretation: Durchschnittlich steigt der Graph um 10 Einheiten, wenn man eine Einheit nach rechts geht.
- - - - - - - - - - - - - - - - - - - - - -
Im folgenden Video wird ein weiteres Beispiel durchgerechnet.
Durchschnittliche Änderungsrate berechnen im Intervall – Differenzenquotient, mittlere Steigung
Lernvideo

Durchschnittliche Änderungsrate berechnen im Intervall – Differenzenquotient, mittlere Steigung

Kanal: MathemaTrick
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen