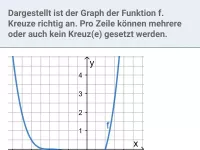
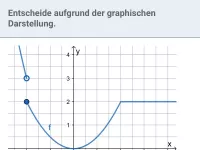
Was lässt sich aus dem Vorzeichen von f ´ (x) ablesen?
Die Ableitung f´ einer differenzierbaren Funktion f liefert für jede definierte Stelle x die lokale Änderungsrate (= Steigung des Graphen von f an dieser Stelle). Insbesondere zeigt das Vorzeichen von f´ an, ob f im betrachteten Intervall zunimmt oder abnimmt:
| f´(x) | f bzw. Gf |
| > 0 | streng monoton zunehmend bzw. wachsend |
| < 0 | streng monoton abnehmend bzw. fallend |
| = 0 | waagrechte Tangente |
Achtung: die Tabelle ist von links nach rechts zu lesen, d.h. aus f´(x)>0 in einem bestimmten Intervall kann auf strenge Monotonie von f geschlossen werden - aber nicht umgekehrt. Wenn f in einem bestimmten Intervall streng monoton wächst, kann es dort durchaus einzelne Stellen geben, an denen die Ableitung gleich null ist (waagrechte Tangente).
Beispiel 1
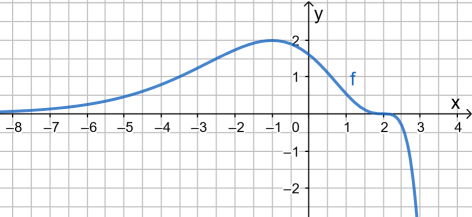
In welchen Intervallen gilt
| > 0, |
| < 0, |
| > 0, |
| < 0? |
An welchen Stellen gilt
| = | 0, |
| = | 0? |
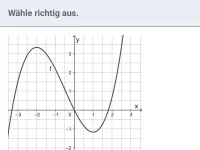
Untersuchung von f
Im Intervall
ist
oberhalb der x-Achse, also
|
G | f |
| > 0. |
Im Intervall
ist
unterhalb der x-Achse, also
|
G | f |
| < 0. |
Bei
schneidet der Graph die x-Achse, also
|
| = | 0. |
Untersuchung von f ´
Im Intervall
ist
streng monoton steigend, also
|
G | f |
| > 0. |
In den Intervallen
und
ist
streng monoton fallend, also
|
|
G | f |
| < 0. |
An den Stellen
und
besitzt der Graph eine waagrechte Tangente, also
und
|
|
| = | 0 |
| = | 0. |

Lernvideo
Lokales und globales Differenzieren, Vorzeichen der Ableitung anhand des Graphen, Beispiel
Kanal: Mathegym
Beispiel 2
Bestimme die Monotonieintervalle der ganzrationalen Funktion f aufgrund der gegebenen ersten Ableitung.
| = |
|
Lösung: Unterteile ℝ gemäß der Nullstellen von f´ (-5 und 0) in Intervalle. Bestimme dann pro Faktor das Vorzeichen in jedem Intervall und daraus das Vorzeichen von f´ in jedem Intervall:
|
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
|
Aus der letzten Zeile ergibt sich schließlich, dass f
- im Intervall [−5;0] streng monoton zunimmt und
- in den Intervallen ]-∞;−5] und [0;∞[ streng monoton abnimmt.
Bemerkung: Manche Schüler wundern sich darüber, dass die Stellen x=−5 und x=0 eingeschlossen werden. Ihrer Meinung nach müssten sie ausgeschlossen sein, da die Ableitung dort Null ist. Schließlich lautet doch das Monotoniekriterium f´(x)>0⇒f wächst streng monoton. Denkfehler dabei: Das Monotoniekriterium gilt nicht "rückwärts", d.h. eine streng monoton steigende Funktion kann durchaus isolierte Stellen mit f´(x)=0 aufweisen. "Streng Monoton steigend" heißt per Definition: Liegt ein Punkt des Graphen rechts von einem anderen, so liegt er höher als dieser. Da macht es gar nichts, wenn der Graph wie hier bei x=−5 eine waagrechte Tangente hat. Entscheidend ist, dass jeder Graphenpunkt rechts von x=−5 im Intervall [−5;0] höher liegt!
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈Oberstufe - Aufgaben + Stoff
Ableitung und Monotonie
Bestimmung von Monotonieintervallen anhand des Graphen und mit Hilfe der ersten Ableitung -
≈Oberstufe - Aufgaben + Stoff + Video
Differenzierbarkeit und Ableitungsfunktion
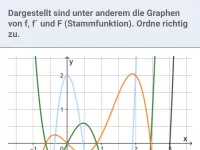
Untersuchung von abschnittsweise definierten Funktionen und Betragsfunktion auf Differenzierbarkeit; Zusammenhang zwischen f, f´ und F (Stammfunktion) anhand von Graphen -
≈Oberstufe - Aufgaben + Stoff + Video
Extremstellen, Extremwerte und Extrempunkte
Lokale und globale Extremstellen ermitteln, Kriterium für lokale Extremstellen
Ähnliche Themen
- Wann ist eine Funktion f an der Stelle x=a nicht differenzierbar?
- Was versteht man unter einer Stammfunktion F von f? Was sagen die Werte von f über F aus?
- Erläutere die "Ableitungskette".
- f´ habe bei x0 eine Nullstelle. Gib alle möglichen Vorzeichenverläufe von f´ in der Umgebung dieser Nullstelle an und wie sich diese jeweils graphisch interpretieren lassen.
- Wie geht man vor, um lokale Maxima und Minima einer Funktion rechnerisch zu bestimmen?
- Woran erkennt man graphisch, dass eine Funktion an einer Stelle nicht differenzierbar ist?
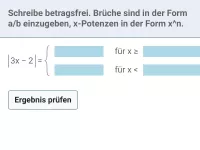
- Wie lässt sich ein Term, der von Betragsstrichen umgeben ist, betragsfrei schreiben?
- Definiere die Begriffe "streng monoton steigend/fallend".