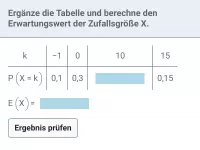
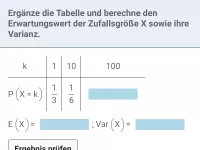
Wie ermittelt man den Erwartungswert einer Zufallsvariablen?
Den Erwartungswert E(X) einer Zufallsvariablen X erhält man, indem man jeden Wert von X mit der zugehörigen Wahrscheinlichkeit multipliziert und daraus die Summe bildet.
Beispiel
Zwei Würfel werden gleichzeitig geworfen. Bei einem 6er-Pasch erhält der Spieler 20€, bei jedem anderen Pasch 5€, ansonsten muss er 2€ zahlen. Lohnt sich dieses Spiel für ihn auf Dauer?
Lösung:
- Wahrscheinlichkeitsberechnungen
| = |
|
| = |
|
| = |
|
- Wahrscheinlichkeitsverteilung der Zufallsgröße G (=Gewinn in €)
|
|
|
| ||||||||||||||||||||||
|
|
|
|
- Erwartungswert als Summe der Spaltenprodukte
| = |
|
| €. |
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was versteht man unter der Varianz einer Zufallsgröße X und wie wird sie berechnet?
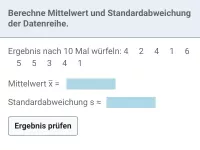
- Was drücken arithmetisches Mittel und Standardabweichung bei einer Datenreihe aus? Wie berechnet man die beiden Größen?
- Was drücken Erwartungswert und Standardabweichung einer Zufallsgröße aus und wie werden sie berechnet?