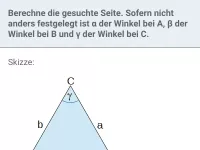
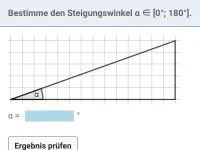
sin, cos und tan im rechtwinkligen Dreieck: wie lauten die drei Formeln?
Sei α ein Winkel < 90° im rechtwinkligen Dreieck. Mit "Gegenkathete" sei die Kathete gemeint, die α gegenüberliegt, mit "Ankathete" diejenige, die an α anliegt. Dann gelten folgende Zusammenhänge:
- sin(α)= Gegenkathete / Hypotenuse
- cos(α)= Ankathete / Hypotenuse
- tan(α)= Gegenkathete / Ankathete
Beispiel 1
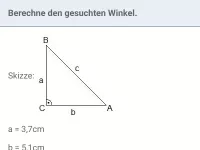
Von einem rechtwinkligen Dreieck mit ∠C = 90° ist bekannt: a = 3 und β = 32°. Berechne die restlichen Seiten und Winkel.
- Skizze (gegebene Größen sind orange markiert)
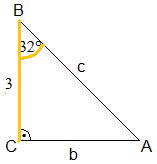
- Berechnung von α:
Wegen der Innenwinkelsumme 180° und des 90°-Winkels bei C gilt:
α = 90° − β = 58°
α = 90° − β = 58°
- Berechnung von b:
b ist die Gegenkathete von ∠B = 32°, außerdem ist die Ankathete gegeben. Benötigt wird also die Formel, in der beide Katheten vorkommen, also Tangens:
| = |
|
| ||||||||||||||||||
| = |
| |||||||||||||||||||
- Berechnung von c:
Nachdem die Katheten a und b bekannt sind, könnte man c mit Hilfe von Pythagoras ausrechnen. Oder man bestimmt die Hypotenuse mit Hilfe von Kosinus, nachdem die Ankathete von ∠B = 32° mit exakter Länge = 3 gegeben ist:
| = |
|
| |||||||||||||||||||
| = |
|
| |||||||||||||||||||
| = |
| ||||||||||||||||||||

Lernvideo
Die Winkelfunktionen Sinus, Kosinus und Tangens I musstewissen Mathe
Kanal: musstewissen Mathe
Beispiel 2
In einem rechtwinkligen Dreieck mit rechtem Winkel bei C ist bekannt: b = 10, c = 11. Berechne β.
Lösung: b ist die Gegenkathete von β, also
| = |
|
| |||||||||||||||||||||
| = |
| ||||||||||||||||||||||
Siehe auch