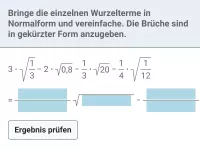
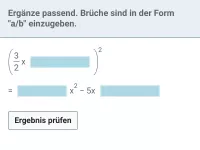
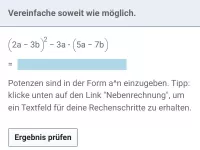
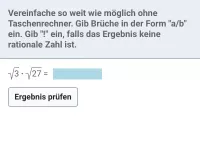
Was versteht man unter Normalform eines Wurzelterms?
Die Normalform eines Wurzelterms erfüllt zwei Bedingungen:
- Die Zahl unter der Wurzel ist quadratfrei, enthält also keinen quadratischen Teiler.
- Unter dem Bruchstrich stehen keine Wurzeln.
Beispiel 1
| Normalform. |
Unter der Wurzel sollten keine Quadrate stehen. 80 enthält die beiden quadratischen Teiler 4 und 16. Man wählt (immer) den größeren und formt um:
| = |
|
Aus der Quadratzahl lässt sich die Wurzel ziehen:
| = |
|
| . |
Beispiel 2
| in Normalform. |
Unter dem Bruchstrich sollte keine Wurzel stehen. Man erreicht dies hier, indem man den Bruch mit √2 erweitert:
| = |
|
Jetzt kann man den Nenner zu 2 vereinfachen. Man erhält die Normalform:
| = |
|
Beispiel 3
| In Normalform. |
Schwieriger ist die Berechnung der Normalform, wenn unter dem Bruchstrich eine Summe (oder Differenz) von Wurzeln steht. Hier ist es die Summe
| . |
In diesem Fall benützt man die 3. binomische Formel, um den Nenner wurzelfrei zu machen:
| = |
|
| erweitern. Man erhält die Normalform: |
| = |
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈9. Klasse - Aufgaben + Stoff + Video
Binomische Formeln
Anwendung Binomischer Formeln zum Multiplizieren von Klammertermen, Faktorisieren, Rationalmachen des Nenners -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratwurzeln - Grundrechenarten, teilweise radizieren
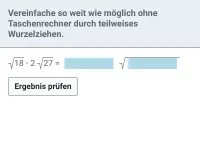
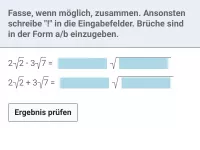
Teilweises Wurzelziehen; Produkte, Summen und Differenzen aus Wurzeltermen vereinfachen -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratwurzeln - Termumformung mit Binomischen Formeln
Anwendung Binomischer Formeln zum Multiplizieren von Klammertermen, Faktorisieren, Rationalmachen des Nenners -
≈9. Klasse - Aufgaben + Stoff + Video
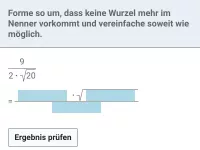
Rationalmachen des Nenners
Rationalmachen des Nenners mittels Erweitern mit einer Quadratwurzel oder unter Anwendung der dritten binomischen Formel mit einer Summe oder einer Differenz von Quadratwurzeln
Ähnliche Themen
- Was ist bei der Addition und Subtraktion von Quadratwurzeln zu beachten?
- Was ist bei der Multiplikation und Division von Quadratwurzeln möglich und welcher Zusammenhang besteht zum teilweisen Radizieren?
- Wie lauten die drei binomischen Formeln?
- Was versteht man unter der Rückwärtsversion der binomischen Formeln und welchen Zweck erfüllt diese?
- Was bedeutet Rationalmachen des Nenners und wie geht man dabei vor?
- Welche Rechenregeln (Grundrechenarten) gelten im Umgang mit Quadratwurzeln und was bedeutet "teilweise radizieren?"