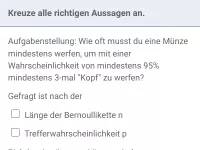
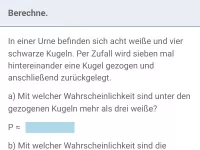
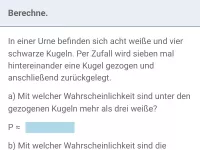
Was versteht man unter Bernoulli-Experiment und Bernoulli-Kette und welcher Zusammenhang besteht zum Binomialkoeffizienten? Wie berechnnet man die Wahrscheinlichkeit eines Pfads der Bernoullikette?

Bernoulli-Experimente und Bernoulli-Ketten:

Bernoulli-Experiment:
Zufallsversuch, bei dem genau zwei mögliche Ergebnisse interessieren, z.B.

  • "Erfolg -- Nichterfolg"
  • "Treffer -- Niete"
  • "0 -- 1".
  • Ist die Treffer-Wahrscheinlichkeit p, so ist die Nicht-Treffer-Wahrscheinlichkeit q = 1− p (Gegenereignis).

Bernoulli-Kette der Länge n:

  • Ein Bernoulli-Experiment wird n mal wiederholt, wobei die Durchführungen jeweils unabhängig voneinander sind.
  • Ein Pfad mit r Treffern hat die Wahrscheinlichkeit pr · qn-r, wobei p die Trefferwahrscheinlichkeit und q = 1 − p die Nicht-Trefferwahrscheinlichkeit ist.
  • In einer Bernoulli-Kette der Länge n gibt der Binomialkoeffizient "n über r" die Anzahl der Pfade mit genau r Treffern an.

Beispiel
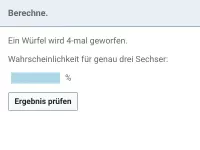
Ein Würfel wird 4 Mal geworfen. Handelt es sich um ein Bernoulli-Experiment? Wenn ja, dann gib Trefferwahrscheinlichkeit und Länge der Bernoulli-Kette an.
Ein Würfel wird 4 Mal geworfen und die Anzahl der geraden Zahlen notiert. Handelt es sich um ein Bernoulli-Experiment? Wenn ja, dann gib Trefferwahrscheinlichkeit und Länge der Bernoulli-Kette an.
Das Werfen eines Würfels ist ein Zufallsexperiment, bei dem jede Durchführung völlig unabhängig vom vorherigen Ausgang ist. Allerdings sind 6 verschiedene Ergebnisse möglich (Zahlen 1 bis 6). Ohne weitere Angaben ist also keine Einteilung in "Treffer" und "Niete" möglich. Es handelt sich nicht um ein Bernoulli-Experiment.
Im zweiten Fall wird das Ereignis "gerade Zahl" betrachtet. Folglich handelt es sich hier um ein Bernoulli-Experiment. Gerade Zahl (2,4,6) gilt als Treffer, ungerade Zahl (1,3,5) als Niete. Die Trefferwahrscheinlichkeit beträgt 1/2. Der Würfel wird vier Mal geworfen, daher ist die Länge der Bernoulli-Kette gleich 4.

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst!

Ähnliche Themen

Online-Übungen und Aufgaben

Online üben und motiviert lernen?

Jetzt unsere Online-Übungen ausprobieren!

  • Keine Registrierung erforderlich!
  • Aufgaben direkt im Browser bearbeiten und lösen.
  • Für die Fächer Mathematik, Latein, Englisch, Chemie und Physik.
Zum Aufgabenbereich