Wie funktioniert der zweiseitige Signifikanztest (Annahmebereich, Signifikanzniveau, Irrtumswahrscheinlichkeit) ?

Zweiseitiger Signifikanztest

Eine Nullhypothese H0: p=p0 wird getestet.

  • Der Annahmebereich liegt symmetrisch um den Erwartungswert.
  • Das Signifikanzniveau α legt die Größe des Annahmebereichs fest.
  • Überschlagsmäßig kann der Annahmebereich mit den Sigma-Regeln bestimmt werden.

Das Gegenteil der Nullhypothese wird als Alternative H1 bezeichnet.

Unter der Irrtumswahrscheinlichkeit versteht man die Wahrscheinlichkeit, die Hypothese zu verwerfen, obwohl sie zutrifft. Sie entspricht der Wahrscheinlichkeit des Ablehnungsbereichs.

Beispiel
H0:
 
p
=
1
2
;
 
H1: p ≠
 
1
2
;
 
n
=
100
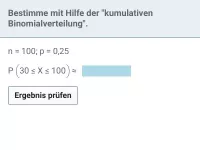
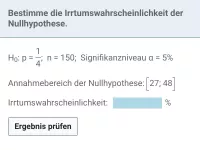
Bestimme für das Signifikanzniveau α = 5% den Annahmebereich zunächst überschlagsmäßig und anschließend genau. Bestimme auch die Irrtumswahrscheinlichkeit.
Lösung:
  • Schritt 1: Annahmebereich überschlagsmäßig bestimmen
Laut der Sigma-Regeln liegt die Trefferzahl mit einer Wahrscheinlichkeit von 95% im Intervall
 
μ-1,96σ ; μ+1,96σ
 
:
μ(X)
=
n
·
p
=
100
·
1
2
=
50
σ(X)
=
n
·
p
·
1
−
p
=
100
·
1
2
·
1
2
=
25
=
5
Daher wird der Annahmebereich ETWA
 
41
;
59
 
sein.
  • Schritt 2: Annahmebereich genau bestimmen
Signifikanzniveau α darf maximal 5% betragen, rechts- und linksseitig also jeweils 2,5%. Daher sind als Intervallgrenzen die kleinsten Zahlen a und b gesucht mit:
P
 
X
 
≤
 
a
=
F
100
;
0,5
 
a
>
0,025
P
 
X
 
≤
 
b
=
F
100
;
0,5
 
b
>
0,975
Die kumulative Binomialverteilung wird anhand einer Tabelle oder des GTR bestimmt. Der überschlagene Annahmebereich aus Schritt 1 kann dabei hilfreich sein:
a = 40, denn:
F
100
;
0,5
 
39
=
0,0176
<
0,025
und
F
100
;
0,5
 
40
=
0,02844
>
0,025
b = 60, denn:
F
100
;
0,5
 
59
=
0,97156
<
0,975
und
F
100
;
0,5
 
60
=
0,9824
>
0,975
Der Annahmebereich der Nullhypothese ist
 
40
;
60
 
.
  • Schritt 3: Irrtumswahrscheinlichkeit bestimmen
Die Irrtumswahrscheinlichkeit entspricht der Wahrscheinlichkeit des Ablehnungsbereichs:
P
 
X
 
≤
 
39
+
P
 
X
 
≥
 
61
=
P
 
X
 
≤
 
39
+
1
−
P
 
X
 
≤
 
60
=
F
100
;
0,5
 
39
+
1
−
F
100
;
0,5
 
60
=
0,0176
+
1
−
0,9824
=
0,0352
 
≈
 
3,5%
Die Irrtumswahrscheinlichkeit ist damit deutlich kleiner als die vorgegebene Grenze von maximal 5% (Signifikanzniveau).
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen