Ein Produkt von Wurzeln lässt sich als Produkt unter einer Wurzel schreiben und umgekehrt. Sofern weder a noch b negativ sind, gilt also
√a · √b = √(a · b)
Ein Quotient von Wurzeln lässt sich als Quotient unter einer Wurzel schreiben und umgekehrt. Sofern weder a noch b negativ sind, gilt also√a : √b = √(a : b)
Nach dem Distributivgesetz können gleiche Wurzeln (bzw. Vielfache davon) addiert und subtrahiert werden:a√c + b√c = (a + b)√c
Achtung: √a + √b ≠ √(a+b)
Oft kann man teilweise die Wurzel ziehen. Sofern a nicht negativ ist, kann man den Faktor a² unabhängig vom Faktor b radizieren:√(a² · b) = √(a²) · √b = a · √b
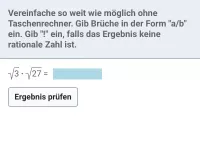
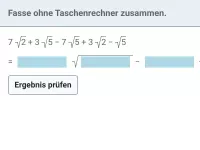
Beispiel 1
| = | ? |
| = | ? |
| = | ? |
|
= |
|
= |
|
= |
|
| − |
|
= |
|
= |
|
= |
|
| − |
|
= |
|
= |
|
= |
|
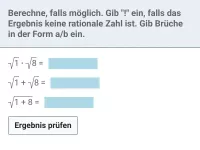
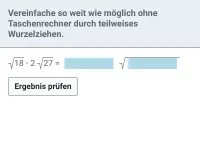
Beispiel 2
| = | ? |
|
= |
|
= |
|
= |
|
= |
|
= |
|
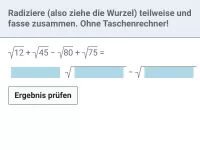
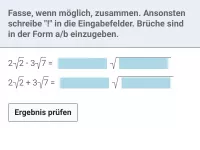
Beispiel 3
| = | ? |
|
= |
|
= |
|
= |
|
= |
|
= |
|
Beispiel 4
| = | ? |
| = | ? |
| = | ? |
|
= |
|
= |
|
| − |
|
= |
|
= |
|
| − |
|
= |
|
= |
|
An diesem Beispiel sieht man sehr schön, dass √a | + | √b ≠ √(a+b) |
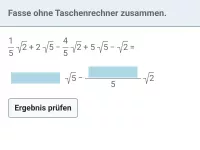
Beispiel 5
| = | ? |
|
|
|
| = |
| Wurzeln zusammenfassen | |||||||||||||||||||||||||||
|
| = |
| kürzen | |||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst!
Weitere Tausende Mathe-Aufgaben...
- Bei uns findest du Online-Übungen zu fast allen Themen der Klassen 5-12.
- Aufgaben direkt im Browser bearbeiten und lösen.
- Für die Fächer Mathematik, Latein, Englisch, Chemie und Physik.
Zum Aufgabenbereich
Und ganz nebenbei: Mathegym wurde ausgezeichnet mit dem "Deutschen Bildungs-Award 2022". Damit belegen wir erneut den 1. Platz bei einem Mathe-Lernportal-Vergleich. Weitere Infos
