Wie erkennt man bei einer Potenzfunktion mit der Funktionsgleichung y=axn, woher der Graph kommt und wohin er geht?
Bei einer Potenzfunktion mit der Funktionsgleichung y=axn entscheidet die Hochzahl n zusammen mit dem Vorfaktor a, von wo der Graph kommt und wohin er geht:
- n ungerade, a positiv (z.B. 5x³): Graph verläuft von links unten nach rechts oben.
- n ungerade, a negativ (z.B. -2x): Graph verläuft von links oben nach rechts unten.
- n gerade, a positiv (z.B. ½x²): Graph verläuft von links oben nach rechts oben.
- n gerade, a negativ (z.B. -x²): Graph verläuft von links unten nach rechts unten.
Beispiel
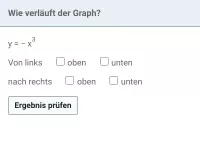
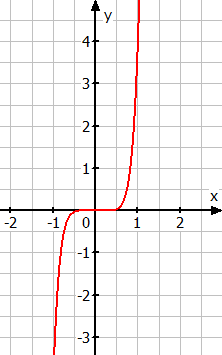
Wie verläuft der Graph?
y | = |
|
y | = |
|
n | = | 7 |
a | = | 4 |
Es handelt sich also um eine Potenzfunktion mit ungerader Hochzahl (7) und positivem Vorfaktor (4). Damit verläuft der Graph von links unten nach rechts oben.
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was ist eine Potenzfunktion und welche Eigenschaften hat diese (abhängig von ihren Parametern)? Welche Spezialfälle sind wohlbekannt?
- Von einem Graphenpunkt ist nur die x- oder y-Koordinate bekannt. Wie ermittelt man die fehlende Koordinate, wenn die Funktionsgleichung vorliegt?
- Wie lassen sich die Schnittpunkte der Graphen zweier Potenzfunktionen ermitteln? Von welcher Gleichung geht man aus und welche Äquivalenzumformungen nimmt man der Reihen nach vor?