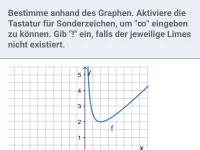
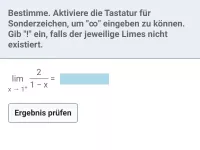
In welcher Form lassen sich Bruchterme evtl. vereinfachen? Nenne drei Techniken, mit deren Hilfe sich diese Form evtl. herstellen lässt.
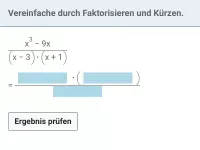
Bruchterme lassen sich evtl. durch Kürzen vereinfachen. Voraussetzung dafür ist, dass Zähler und Nenner in Produktform, also faktorisiert, vorliegen. Oft muss man diese Faktorisierung erst einmal vornehmen, bevor man kürzt. Folgende Techniken helfen dabei am häufigsten weiter:
- Ausklammern von x bzw. einer Potenz von x, z.B. bei x³−4x²+x
- Binomische Formeln
- Lösungsformel für qudratische Gleichung oder auch Satz von Vieta
Siehe auch