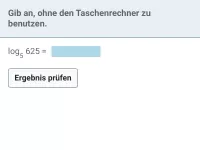
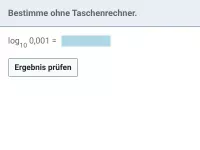
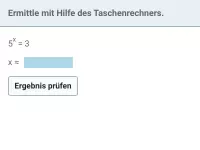
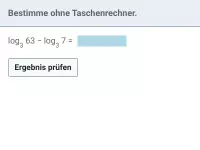
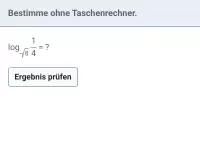
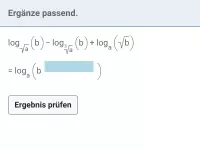
log br (a) Wie lässt sich dieser Logarithmus, bei dem die Basis eine Potenz ist, umformen?
Ist die Basis des Logarithmus eine Potenz br, so lässt sich der Logarithmus wie folgt umformen:
log br (a) = log b (a1/r)
Beispiel
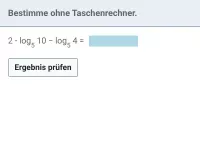
Vereinfache.
| = | ? |
Lösung: Bringe zunächst beide Logarithmen auf die Basis a und vereinfache dann.
| = |
|
| = |
|
Jetzt kann man die Logarithmus-Rechenregeln anwenden und vereinfachen:
|
|
= |
|
= |
|
= |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie lässt sich der Wert von logb a deuten?
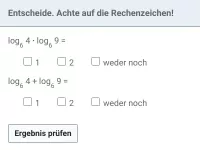
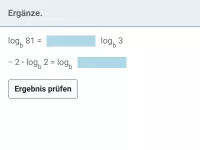
- Bei welchen Rechenarten und welcher Bedingung lassen sich mehrere Logarithmen zu einem Logarithmus zusammenfassen und wie genau lautet die Regel?
- Welche Umformung ist möglich, wenn das Argument des Logarithmus eine Potenz ist?
- Wie lässt sich logb a mit dem TR berechnen, wenn du dort nur eine "log" Taste (Zehnerlogarithmus) hast?
- Was versteht man unter einer Exponentialgleichung und wie löst man sie?
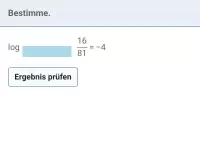
- Welche Umformung kann dazu beitragen, logb (a) ohne Taschenrechner zu bestimmen?
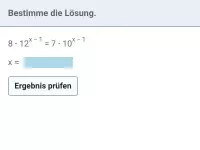
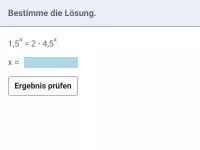
- bT1(x) = bT2(x) [ T1(x) und T2(x) sind x-Terme ] Wie lässt sich so eine Gleichung lösen?
- logb a = c Wie geht man am besten vor, wenn a oder b gesucht sind?
- Wie geht man beim Lösen einer Exponentialgleichung vor, in der nur eine Potenz und sonst kein weiteres x vorkommt?
- Wie lassen sich Summen oder Differenzen von Potenzen (mit x im Exponenten) evtl. vereinfachen?