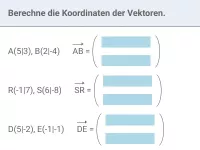
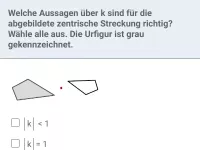
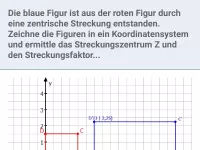
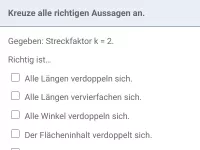
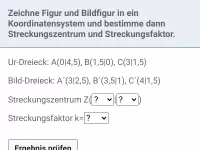
Wie lässt sich bei einer zentrischen Streckung mit Hilfe von Vektoren der Punkt P, der Bildpunkt P' oder der Streckungsfaktor k ermitteln?
Zentrische Streckung mit Zentrum Z: Um den Streckungsfaktor k, den Punkt P oder den Bildpunkt P' zu ermitteln, gehst du im Prinzip immer gleich vor:
- Bilde den Verbindungsvektor von Z und P', ebenso den von Z und P
- Der erste Vektor ist gleich "k mal" der zweite (Gleichung)
- Die Vektorgleichung kann jetzt in zwei Gleichungen aufgespaltet werden
- Schließlich kann nach k oder den gesuchten Koordinaten aufgelöst werden
Beispiel 1
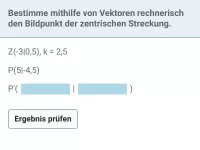
Beispiel Bildpunkt:
Z(-1|1),
, P(2|-3), bestimme den Bildpunkt P'(x'|y').
k | = | 4 |
ZP'
| = |
|
| = |
|
Aufspalten in zwei Gleichungen:
| = |
| |||||||||||||||||||||||
| = |
| |||||||||||||||||||||||
Gleichungen nach x' bzw. y' auflösen:
| = | 11 |
| = |
|
Damit hat der Bildpunkt die Koordinaten P'(11|-15).
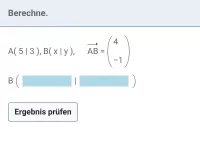
Beispiel 2
Beispiel Urpunkt:
Z(-3|1),
, P'(5|-4), bestimme den Urpunkt P(x|y).
k | = | 2 |
ZP'
| = |
|
| = |
|
Aufspalten in zwei Gleichungen:
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
Gleichungen nach x bzw. y auflösen:
| = | 1 |
| = |
|
Damit hat der Urpunkt die Koordinaten P(1|-1,5).
Beispiel 3
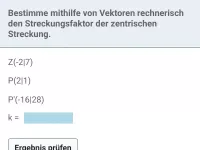
Beispiel Streckungsfaktor:
Z(2|4), P(1|1), P'(5|13) bestimme den Streckungsfaktor .
k
ZP'
| = |
|
| = |
|
Aufspalten in zwei Gleichungen:
| = |
| ||||||||||||||
| = |
| ||||||||||||||
Gleichungen jeweils nach k auflösen:
| = | k |
| = | k |
Weil für k jeweils die gleiche Zahl herauskommt, ist es eine zentrische Streckung mit dem Streckungsfaktor
.
k | = |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈7. Klasse - Aufgaben + Stoff + Video
Vektoren (zweidimensional)
Vektorkoordinaten berechnen, Rechnen mit Vektoren, Parallelverschiebung -
≈8. Klasse - Aufgaben + Stoff + Video
Zentrische Streckung
Zentrische Streckung einer Figur bei gegebenem Zentrum Z und Streckungsfaktor k. Ermittlung von Z und k anhand gegebener Figur und Bildfigur; Eigenschaften der zentrischen Streckung
Ähnliche Themen
- Statt zwei Parallelverschiebungen hintereinander kann man auch eine Parallelverschiebung durchführen. Wie lassen sich die Koordinaten des entsprechenden Vektors ermitteln?
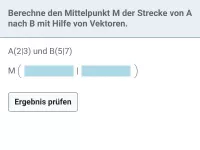
- Wie berechnet man den Mittelpunkt einer Strecke AB?
- Was ist eine zentrische Streckung, welche Eigenschaften haben Figur und Bildfigur und was sagt der Streckungsfaktor k aus?
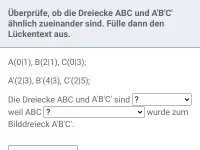
- Welche Eigenschaften haben ähnliche Dreiecke?
- Was ist eine zentrische Streckung, welche Eigenschaften haben Figur und Bildfigur und was sagt der Streckungsfaktor k aus?
- Was gilt für Vektor und Urvektor bei einer zentrischen Steckung bzgl. Länge und Richtung? Wie erhält man die Koordinaten des Bildvektors?
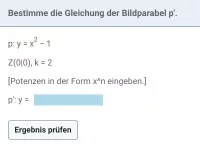
- Wie erhältst du bei einer zentrischen Streckung mit Hilfe von Vektoren die Gleichung einer Bildgerade oder Bildparabel (wenn Urgerade bzw. Urparabel durch ihre Gleichung gegeben sind)?