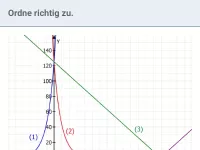
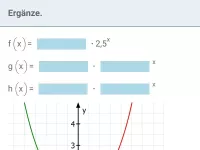
f(x) = b·ax Bei welchen Werten von a und b schneidet der Graph die y-Achse im positiven Bereich und steigt an/fällt? Was passiert, wenn man b durch −b ersetzt? Was passiert, wenn man a durch 1/a ersetzt?

Ist f(x) = b·ax, so gilt für
  • b>0 und a>1:
    der zugehörige Graph schneidet die y-Achse im positiven Bereich und steigt an (umso steiler, je größer a)
  • b>0 und 0<a<1:
    der zugehörige Graph schneidet die y-Achse im positiven Bereich und fällt (umso steiler, je kleiner a)
  • g(x) = −b·ax:
    der Graph von g entsteht, indem man den Graphen von f an der x-Achse spiegelt
  • h(x) = b·(1/a)x:
    der Graph von h entsteht, indem man den Graphen von f an der y-Achse spiegelt
Beispiel
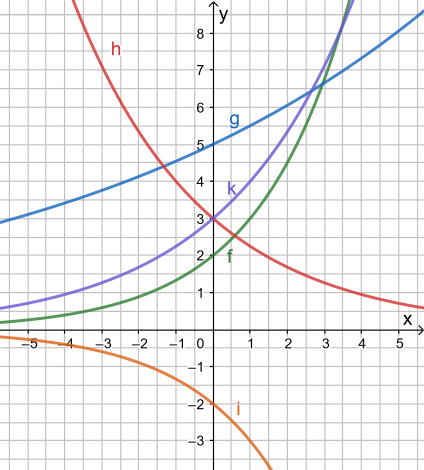
Skizziere die Graphen folgender Funktionen:
f
 
x
=
2
·
1,5
x
     
g
 
x
=
5
·
1,1
x
     
h
 
x
=
3
·
3
4
x
     
i
 
x
=
−
2
·
1,5
x
     
k
 
x
=
3
·
4
3
x
Wo ergeben sich welche Symmetrien? Welche Funktion wächst am stärksten?
Bei f, g und k liegt exponentielles Wachstum vor (Wachstumsfaktor a jeweils größer als 1), also steigen die zugehörigen Graphen. Der Anstieg nimmt umso stärker zu, je größer a ist. Daher nimmt der Anstieg bei 
G
g
 am wenigsten zu 
a
=
1,1
 und bei 
G
f
 am stärksten 
a
=
1,5
. Zu beachten sind auch die Anfangsbestände zum Zeitpunkt 
x
=
0:
 
G
f
 schneidet die y-Achse in (0|2), 
G
g
 schneidet die y-Achse in (0|5) und 
G
k
 schneidet die y-Achse in (0|3).
Bei h liegt exponentieller Rückgang vor 
3
4
 
<
 
1
, also muss 
G
h
 fallen. Es fällt auf, dass  
3
4
 der Kehrwert von 
4
3
, also dem Wachstumsfaktor von k ist und dass h und k auch im Anfangsbestand 3 übereinstimmen. Daher ergibt sich 
G
h
 aus 
G
k
 durch Spiegelung an der y-Achse.
Schließlich ergibt sich 
G
i
 aus 
G
f
 durch Spiegelung an der x-Achse, da 
i
x
=
−
f
x
.
graphik
Exponentialfunktionen
Lernvideo

Exponentialfunktionen

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen