Mechanik - senkrechter Wurf
Senkrechter Wurf nach oben - Gesamtaufgabenbestand (lehrplanunabhängig)

Lernvideo
Senkrechter Wurf
Kanal: LEIFIphysik
Senkrechter Wurf
Das Wurfobjekt wird aus einer Anfangshöhe \(y_0\) mit einer Anfangsgeschwindigkeit \(v_0\) senkrecht nach oben geworfen.
Formeln:
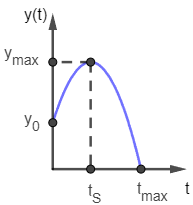
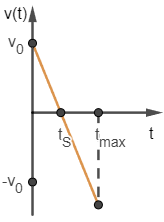
Das Wurfobjekt wird aus einer Anfangshöhe \(y_0\) mit einer Anfangsgeschwindigkeit \(v_0\) senkrecht nach oben geworfen.
- Das Wurfobjekt wird auf seinem Weg nach oben aufgrund der Erdbeschleunigung \(g\), die nach unten wirkt, abgebremst.
- Nach der Steigzeit \(t_S\) erreicht das Objekt im Umkehrpunkt seine maximale Höhe \(y_{max}\). Im Umkehrpunkt ist seine Geschwindigkeit null.
- Dann fällt das Wurfobjekt gleichmäßig beschleunigt nach unten, bis es nach der Gesamtzeit \(t_{max}\) bzw. \(t_{ges}\) am Boden auftrifft.
Formeln:
- Geschwindigkeit in Abhängigkeit der Zeit:
\(\colorbox{#E8EFF5}{\(v(t) = v_0 - g \ t\)}\) - Höhe in Abhängigkeit der Zeit:
\(\colorbox{#E8EFF5}{\(y(t) = y_0 + v_0 \ t - \dfrac 12 \ g \ t^2\)}\)


Beispiel
Ein Ball wird vom Boden aus senkrecht nach oben geworfen und erreicht nach \(10,0\ s\) wieder die Abwurfstelle. Berechne die Steigzeit \(t_S\), die Abwurfgeschwindigkeit \(v_0\) und die maximale Höhe \(y_{max}\).
Gesamtenergie beim senkrechten Wurf
Befindet sich das Wurfobjekt in der Höher \(y(t)\) und hat die momentane Geschwindigkeit \(v(t)\), so gilt für die Gesamtenergie (ohne Reibung):
\(\colorbox{#E8EFF5}{\(E=m\ g\ y(t) + \dfrac 12 m\ v(t)^2\)}\)
Formel angewendet in den speziellen Punkten:
Abwurf:
\(\colorbox{#E8EFF5}{\(E=m\ g\ y_0 + \dfrac 12 m\ v_0^2\)}\)
Umkehrpunkt:
\(\colorbox{#E8EFF5}{\(E=m\ g\ y_{max}\)}\)
Aufprall:
\(\colorbox{#E8EFF5}{\(E=\dfrac 12 m\ v_{max}^2\)}\)
mit
Befindet sich das Wurfobjekt in der Höher \(y(t)\) und hat die momentane Geschwindigkeit \(v(t)\), so gilt für die Gesamtenergie (ohne Reibung):
\(\colorbox{#E8EFF5}{\(E=m\ g\ y(t) + \dfrac 12 m\ v(t)^2\)}\)
Formel angewendet in den speziellen Punkten:
Abwurf:
\(\colorbox{#E8EFF5}{\(E=m\ g\ y_0 + \dfrac 12 m\ v_0^2\)}\)
Umkehrpunkt:
\(\colorbox{#E8EFF5}{\(E=m\ g\ y_{max}\)}\)
Aufprall:
\(\colorbox{#E8EFF5}{\(E=\dfrac 12 m\ v_{max}^2\)}\)
mit
| \(y_0\) | Anfangs-/Abwurfhöhe |
| \(y_{max}\) | maximale Höhe / Umkehrpunkt |
| \(v_0\) | Anfangs-/Abwurfgeschwindigkeit |
| \(v_{max}\) | End-/Aufprallgeschwindigkeit |
| \(m\) | Masse |
| \(g\) | Erdbeschleunigung |
Beispiel
Ein Ball erreicht beim senkrechten Wurf nach oben (Abwurfgeschwindigkeit \(v_0=44\dfrac ms\)) eine maximale Flughöhe von \(120\ m\).
Berechne...
Berechne...
- die Abwurfhöhe \(y_0\),
- die Endgeschwindigkeit \(v_{max}\),
- die Geschwindigkeit in \(60\ m\) Höhe.

