Flächeninhalt von Parallelogramm, Dreieck und Trapez

Flächenberechnung von Parallelogramm, Dreieck und Trapez sowie Figuren, die sich daraus zusammensetzen; Oberflächenberechnung von Quader, Prisma und Pyramide sowie Körpern, die sich daraus zusammensetzen - Lehrplan G9 (5.-12. Klasse)

Flächenberechnung (Teil 1)
Lernvideo

Flächenberechnung (Teil 1)

Kanal: Mathegym
Flächenberechnung (Teil 2)
Lernvideo

Flächenberechnung (Teil 2)

Kanal: Mathegym
Wie berechnet man Fläche und Umfang eines Dreiecks?
#63
Ein Dreieck mit den Seitenlängen a, b und c
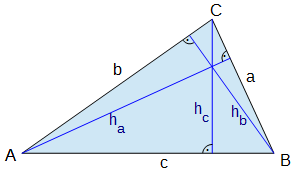
und den zugehörigen Höhen ha, hb und hc hat
  • den Umfang U = a + b + c
  • den Flächeninhalt A = ½ · a · ha = ½ · b · hb = ½ · c · hc

Achte bei der Rechnung darauf, dass alle Größen in derselben Einheit angegeben sind (evtl. umwandeln!)

Beispiel 1
Gegeben ist ein Dreieck ABC mit
 
a
=
48 cm, b
=
63 cm, c
=
5,5 dm, h
c
=
460 mm
 
.
Gesucht sind die Fläche A und der Umfang U.
Beispiel 2
Gegeben ist ein Dreieck mit folgenden (gerundeten) Angaben:
h
b
=
5,8 cm
;
h
c
=
5,5 cm
;
A
=
20,1 cm
2
;
U
=
20,6 cm
Bestimme daraus die Seiten a, b und c.
Wie berechnet man Fläche und Umfang eines Parallelogramms?
#62
Ein Parallelogramm mit den Seitenlängen a und b und den zugehörigen Höhen ha und hb hat
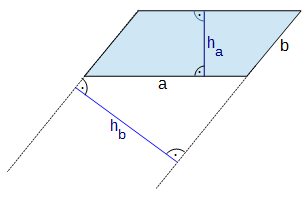
  • den Umfang U = 2 · ( a + b )
  • den Flächeninhalt A = a · ha = b · hb

Achte bei der Rechnung darauf, dass alle Größen in derselben Einheit angegeben sind (evtl. davor umwandeln).

Beispiel 1
Gegeben ist ein Parallelogramm mit
 
a
=
210 mm, b
=
18 cm, h
a
=
15,1 cm
 
.
Gesucht:
 
Fläche A und Umfang U
Beispiel 2
Berechne die Fläche des Parallelogramms mit den Eckpunkten A(-3|-1), B(2|-1), C(5|1), D(?|?)
Beispiel 3
Gegeben ist ein Parallelogramm mit folgenden Angaben:
Fläche A
=
34,3 cm
2
;
Höhe h
a
=
7 cm
;
Seite b
=
9,2 cm
Bestimme daraus die Seite a und den Umfang U.
Wie berechnet man den Flächeninhalt eines Trapezes?
#64
Ein Trapez mit den parallelen Seiten a und c und der Höhe h hat den Flächeninhalt

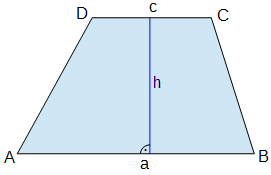
A = ½ · (a + c) · h

Achte bei der Rechnung darauf, dass alle Größen in derselben Einheit angegeben sind (evtl. umwandeln!)

Beispiel
Gegeben ist ein Trapez (a || c) mit
 
a
=
5,2 cm, b
=
4,1 cm, c
=
27 mm, d
=
0,41 dm, h
=
0,4 dm
Bestimme die Fläche A und den Umfang U.
Welche Figuren bilden die Oberfläche eines Prismas?
#69
Die Oberfläche eines Prismas setzt sich aus mehreren Teilflächen zusammen:
  • Grund und Deckfläche des Prismas sind gleich und können z.B. dreieckig oder trapezförmig sein.
  • Die Seitenwände sind allesamt rechteckig, aber normalerweise nicht gleich.
Beispiel
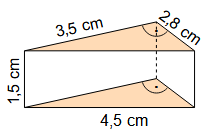
graphik
O
=
?
Mathe üben

Beispielaufgaben zum Selberrechnen

Wir haben für dich 82 Mathe-Aufgaben zum Thema Flächeninhalt von Parallelogramm, Dreieck und Trapez, die du bei uns online rechnen und lösen kannst.
Aufgaben rechnen