Achsenspiegelung und Symmetrie - Konstruktion
Spiegelbild kontruieren, Konstruktion von Mittelsenkrechter und Winkelhalbierender - Lehrplan
Welche einzigartige Eigenschaft besitzen Punkte auf der Symmetrieachse bezüglich eines Punkts P und seines Spiegelpunkts P´?
#385
Punkte, die auf der Symmetrieachse liegen, haben eine exklusive Eigenschaft (d.h. nur sie haben diese Eigenschaft): Sie sind zu symmetrischen Punkten gleich weit entfernt. D.h.
- sind P und P´ zueinander achsensymmetrische Punkte und A ein beliebiger Punkt der Achse, so ist dieser zu P und P´gleich weit entfernt.
- sind P und P´ zueinander achsensymmetrische Punkte und von A gleich weit entfernt, so muss A auf der Spiegelachse liegen.
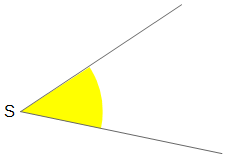
Beispiel 1
Ein Winkel soll halbiert werden.
Beispiel 2
(A) Von P aus soll ein Lot auf g gefällt werden (P ∉ g).
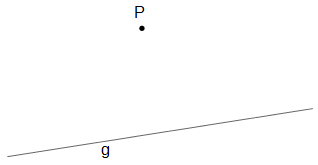
(B) Im Punkt P soll ein Lot zur Geraden g errichtet werden (P ∈ g).

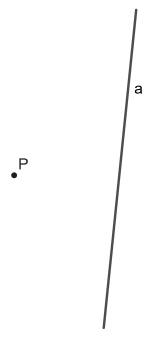
Beispiel 3
Der Punkt P soll an der Achse a gespiegelt werden.