Geometrie - Thaleskreis/Peripheriewinkelsatz
- Lehrplan für 8.-9. Jgst
Was besagt der Satz des Thales und was ist der Thaleskreis?
#787
Satz des Thales:
- Liegen A, B und C auf einem Kreis und geht AB durch den Mittelpunkt, so ist das Dreieck ABC bei C rechtwinklig. Man spricht vom "Thaleskreis" über AB.
- Umgekehrt gilt: ist das Dreieck ABC bei C rechtwinklig, so liegt C auf dem Thaleskreis über AB.
Beispiel 1
Welche der folgenden Dreiecke sind rechtwinklig?
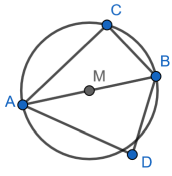
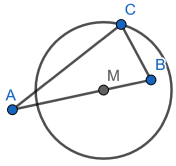
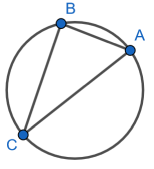
Beispiel 2
Ermittle durch Konstruktion alle Punkte, von denen aus die beiden Strecken a und b unter einem rechten Winkel erscheinen.
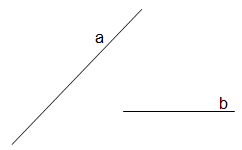
Ein Kreis wird durch eine Sehne a in zwei Bögen unterteilt. Man betrachte den größeren der beiden Bögen (falls gleichgroß: einen der beiden Halbkreise):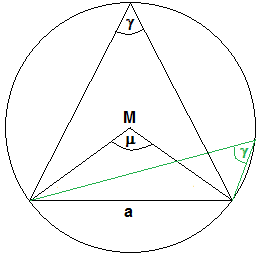
- Von jedem Punkt des sogenannten Fasskreisbogens erscheint die Sehne unter demselben Winkel γ (Randwinkel oder Umfangswinkel).
- Vom Kreismittelpunkt aus erscheint die Sehne dagegen unter dem Winkel µ = 2γ, d.h. der Mittelpunktswinkel ist immer doppelt so groß wie der Umfangswinkel.
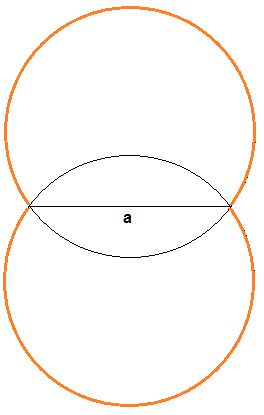
- Durch Spiegelung an a erhält man den zweiten Fasskreisbogen (zweites Bild). Das Fasskreisbogenpaar (die Sehnenendpunkte gehören nicht dazu) ist also der geometrische Ort aller Punkte, von denen aus a unter demselben Winkel erscheint.
- Im Spezialfall a = Durchmesser (s.o.) ergänzen sich die Fasskreisbögen (Halbkreise) zum Thaleskreis, der Randwinkel beträgt also hier stets 90°.



