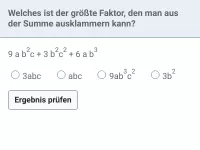
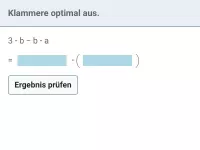
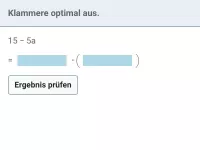
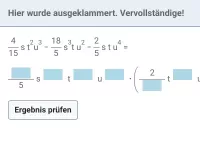
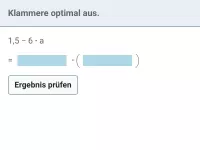
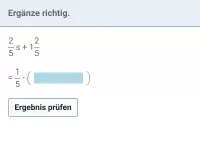
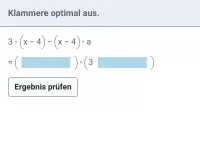
Wie funktioniert Ausklammern?

Enthält jeder einzelne Summand einer Summe denselben Faktor, so kann man diesen ausklammern, also als Faktor vor die Summenklammer schreiben (Distributivgesetz "rückwärts"):

a · b + a · c = a · (b + c)

(Ebenso mit − statt +)

Beispiel 1
Klammere so viele Faktoren wie möglich aus:
14a
2
b
3
−
21ab
2
+
42ab
3
- - - - - - - - - - - - - - - - - in allen Zahlen steckt 7 als (größter gemeinsamer) Teiler:
2
·
7
 
a
2
b
3
−
3
·
7
 
ab
2
+
6
·
7
 
ab
3
=
- - - - - - - - - - - - - - - - - 7 ausklammern:
7
·
2a
2
b
3
−
3ab
2
+
6ab
3
=
- - - - - - - - - - - - - - - - - in allen Summanden steckt a als Teiler (größtmögliche Potenz):
7
·
2
 
a
·
a
 
b
3
−
3
 
a
 
b
2
+
6
 
a
 
b
3
=
- - - - - - - - - - - - - - - - - a ausklammern:
7
 
a
 
2a
 
b
3
−
3b
2
+
6b
3
=
- - - - - - - - - - - - - - - - - in allen Summanden steckt b² als Teiler (größtmögliche Potenz):
7a
 
2a
 
b
2
·
b
−
3
 
b
2
+
6
 
b
2
·
b
=
- - - - - - - - - - - - - - - - - b² ausklammern:
7a
 
b
2
 
2ab
−
3
+
6b
Zusätzliche Erklärungen findest du in folgenden Videos
:
Beispiel 2
Gib größtmögliche Zahlen/Potenzen an, die ausgeklammert werden können:
−
18
 
x
2
y
3
z
+
54
 
x
 
y
2
z
+
27
 
x
4
y
5
  • Betrachtung der Zahlen:
18, 54 und 27 enthalten
 
9
 
als größten gemeinsamen Teiler.
  • Betrachtung der x-Potenzen:
x
2
 
, x und x
4
enthalten
 
x
 
als größten gemeinsamen Teiler.
  • Betrachtung der y-Potenzen:
y
3
 
, y
2
und y
5
enthalten
 
y
2
 
als größten gemeinsamen Teiler.
  • Betrachtung der z-Potenzen:
Der letzte Summand enthält keine z-Potenz.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Insgesamt:
Es kann also
 
9xy
2
 
ausgeklammert werden.
Beispiel 3
Klammere so aus, dass in der Klammer betragsmäßig möglichst kleine ganze Zahlen stehen:
8
9
 
z
+
4
2
3
Beachte, dass mit der gemischten Zahl
 
4
2
3
 
die Summe 4
+
2
3
 
gemeint ist.
Lösung:
8
9
 
z
+
4
2
3
=
8
9
 
z
+
14
3
=
8
9
 
z
+
42
9
=
2
9
·
4z
+
2
9
·
21
=
2
9
 
4z
+
21
Beispiel 4
110
−
z
·
44
=
22
·
5
−
22
·
2z
=
22
·
5
−
2z
Beispiel 5
 
 
38
·
z
−
z
·
19
·
x
=
19
·
2
·
z
−
z
·
19
·
x
=
19
·
z
·
2
−
19
·
z
·
x
=
19z
·
2
−
x

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst!

Ähnliche Themen

Online-Übungen und Aufgaben

Online üben und motiviert lernen?

Jetzt unsere Online-Übungen ausprobieren!

  • Keine Registrierung erforderlich!
  • Aufgaben direkt im Browser bearbeiten und lösen.
  • Für die Fächer Mathematik, Latein, Englisch, Chemie und Physik.
Zum Aufgabenbereich