Wie ist das Pascalsche Dreieck aufgebaut und wofür wird es verwendet?
Aufbau des pascalschen Dreiecks:
Verwendung des pascalschen Dreiecks:
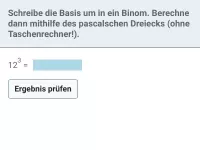
Mithilfe des pascalschen Dreiecks kann man schnell beliebige ganzzahlige Potenzen von Binomen ausmultiplizieren.
Denn:
In Zeile n des pascalschen Dreiecks stehen die Koeffizienten, die zur Berechnung von (…)n benötigt werden.
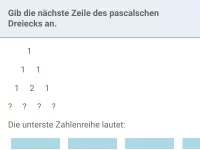
- In der obersten Zeile des pascalschen Dreiecks (n = 0) steht eine 1.
- In der Zeile darunter (n = 1) stehen zwei 1er.
- Die Einträge am linken und rechten Rand sind jeweils 1.
- Die anderen Einträge sind jeweils die Summe der zwei darüberstehenden Einträge.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
usw.
Verwendung des pascalschen Dreiecks:
Mithilfe des pascalschen Dreiecks kann man schnell beliebige ganzzahlige Potenzen von Binomen ausmultiplizieren.
Denn:
In Zeile n des pascalschen Dreiecks stehen die Koeffizienten, die zur Berechnung von (…)n benötigt werden.
Beispiel
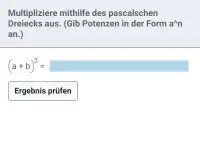
Multipliziere mithilfe des pascalschen Dreiecks aus:
| = | ? |
| = | ? |
Jeder Summand des ausmultiplizierten Binoms besteht aus einem Koeffizienten, einer Potenz von a und einer Potenz von b. Die Koeffizienten werden aus Zeile n des pascalschen Dreiecks abgelesen. Die Potenzen von a nehmen von links nach rechts ab, die Potenzen von b nehmen von links nach rechts zu.
- Potenzen von a
Exponent des Binoms ist 2, daher sind die Potenzen von a von links nach rechts:
|
|
Vereinfacht:
| 1 |
- Potenzen von b
Exponent des Binoms ist 2, daher sind die Potenzen von b von links nach rechts:
|
|
Vereinfacht:
|
|
- Koeffizienten
Die Koeffizienten liest man aus Zeile 2 des pascalschen Dreiecks ab:
| 1 |
- Vorzeichen
Ist das Binom eine Summe, werden alle Teilterme durch + verbunden.
Ist das Binom eine Differenz, wechseln sich + und − ab, wobei immer ein Minus steht, wenn im folgenden Teilterm der Exponent von b ungerade ist.
Also:
| 2 |
= |
|
= |
|
Genauso ergibt sich:
| 2 |
= |
|
= |
|
Siehe auch