Wie wird die Gesamtänderung einer Größe G(t) bei bekannter Änderungsrate G'(t) berechnet?
Manchmal ist im Sachzusammenhang nur die zeitliche Änderungsrate G'(t) einer Größe G(t) bekannt. Oft ist dann für zwei gegebene Zeitpunkte a und b von Interesse, welche Gesamtänderung ΔG = G(b) - G(a) die Größe G innerhalb der durch [a; b] gegebenen Zeitspanne aufweist.
Die Gesamtänderung kann in diesem Fall als Integral über G'(t) mit Untergrenze a und Obergrenze b berechnet werden und entspricht graphisch der Flächenbilanz der im Intervall [a; b] von der t-Achse und dem Graphen von G' begrenzten (und positiv bzw. negativ orientierten) Flächen.
Beispiel 1
In einer Fertigungshalle bewegt sich ein Roboter auf geradlinigen Schienen nach rechts oder links. Für einen bestimmten Fertigungsschritt muss der Roboter seine Position
wie in der folgenden Abbildung dargestellt ändern:
x |
|
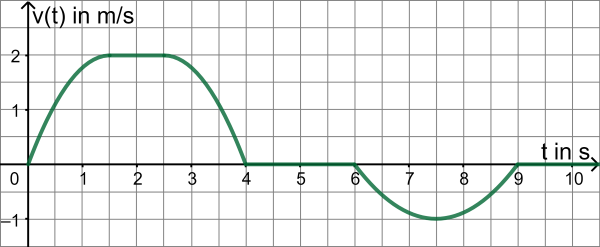
Dabei ist
die Änderungsrate der Roboterposition in
und t die Zeit seit Beginn des Fertigungsschritts in Sekunden. Positive Werte von v stehen für Bewegungen nach rechts, negative für Bewegungen nach links. Zu Beginn steht der Roboter
vom linken Ende der Schienen entfernt.
v |
|
m |
s |
3 | m |
Bestimme die Endposition des Roboters und die von ihm insgesamt zurückgelegte Strecke.
v ist die Änderungsrate der Roboterposition. Die Gesamtänderung der Position ist daher das Integral über v, d.h. die Bilanz orientierter Flächeninhalte zwischen t-Achse und Graph:

Der Flächeninhalt von einem Kästchen unter dem Graphen in der Abbildung entspricht einer Positionsänderung um
Weil der Roboter zu Beginn
vom linken Ende der Schienen entfernt steht, und weil Flächen unter der t-Achse negativ orientiert sind, ergibt sich durch "Kästchenzählen" als p des Roboters:
| = |
|
3 | m |
Endposition
| = |
| ||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||
Am Ende des Fertigungsschritts steht der Roboter
vom linken Ende der Schienen entfernt.
|
Für die insgesamt
s müssen die Positionsänderungen hingegen betragsmäßig berücksichtigt werden:
zurückgelegte | Strecke |
| = |
| |||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||
Die insgesamt zurückgelegte Strecke beträgt
| . |
Beispiel 2
An einem Flüssiggasterminal wird ein voll beladener LNG-Tanker innerhalb von 20 Stunden vollständig entladen. Der Vorgang wird näherungsweise durch die in ℝ definierte Funktion R mit
modelliert. Dabei ist
die Zeit in Stunden ab dem Beginn der Entladung und
die Entladerate in Kubikmetern pro Stunde.
| = |
|
| 20] |
R |
|
Berechne im Rahmen dieses Modells die Ladekapazität des LNG-Tankers.
Weil
die Änderungsrate der Tankerladung ist, ergibt sich die Gesamtänderung der Flüssiggasmenge im Tanker also aus dem Integral:
R |
|
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Weil der Betrag dieser Gesamtänderung der anfänglichen Beladung und damit auch der Ladekapazität des LNG-Tankers entspricht, beträgt diese
| . |
Siehe auch
