Wie berechnet man das Volumen und die Oberfläche einer Kugel?
Eine Kugel mit dem Radius r besitzt
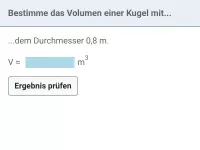
- das Volumen V = 4/3 · r³ · π
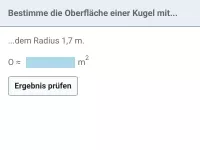
- den Oberflächeninhalt O = 4 · r² · π
Beispiel 1
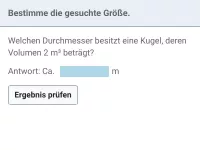
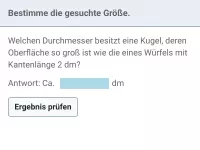
Welchen Durchmesser muss ein kugelförmiges Gefäß mindestens haben, wenn es einen Hektoliter Flüssigkeit beinhaltet?
Lösung: Setze in die Volumenformel das gegebene Volumen (100 Liter = 100 dm³) ein und löse nach r auf.
| = |
| ||||||||||||||||||||
| = |
|
| |||||||||||||||||||
| = |
|
| |||||||||||||||||||
| = |
| ||||||||||||||||||||
Da nach dem Durchmesser gefragt wird, muss man den Wert noch verdoppeln; es ergibt sich ein Durchmesser von mindestens 5,8 dm = 58 cm.
Beispiel 2
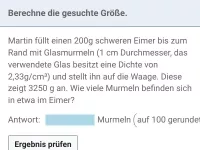
In einer Schachtel (Leergewicht 75 g) stecken 1000 kleine Eisenkugeln (Dichte von Eisen: 7,874 g/cm³) mit einem Durchmesser von jeweils 1 cm. Wie viel wiegt die volle Schachtel?
Lösung: Berechne zunächst das Volumen einer Eisenkugel, multipliziere dieses Ergebnis mit 1000 und schließlich noch mit der Dichte von Eisen, um die Masse aller Kugeln zu erhalten. Dazu ist dann noch die Masse der Schachtel zu addieren
| = |
|
| 4123 g |
| = | 4198 g |
Die Wage zeigt also ca. 4,2 kg an.
Beispiel 3
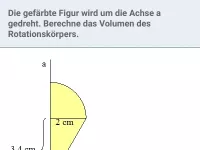
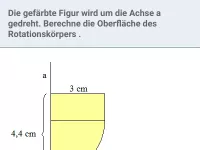
Die gefärbte Figur wird um die Achse a gedreht. Berechne Volumen und Oberfläche des Rotationskörpers.
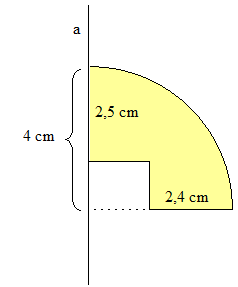
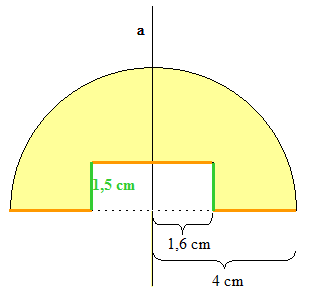
Lösung: Dreht man die gefärbte Figur um die Achse a, so entsteht eine Halbkugel mit Radius r K = 4 cm, aus der (von unten) ein Zylinder mit Radius r Z = 1,6 cm und Höhe h = 1,5 cm herausgebohrt wurde.
- Volumen
Ziehe vom Volumen der Halbkugel das Volumen des Zylinders ab, um das Volumen des Körpers zu erhalten.
| = |
|
| = |
|
| = |
|
- Oberfläche
Ohne Ausbohrung würde sich die Oberfläche der Halbkugel aus der halben Kugeloberfläche und der kreisförmigen Grundfläche G zusammensetzen. G bleibt nach der Ausbohrung im Prinzip erhalten (orange), HINZU kommt die Mantelfläche des Zylinders (grün). Die Oberfläche des Köpers ergibt sich also durch ADDITION dieser drei Teilflächen.
| = |
|
| = |
|
| = |
|
| = |
|

Lernvideo
Oberfläche des Drehkörpers
Kanal: Mathegym
Siehe auch