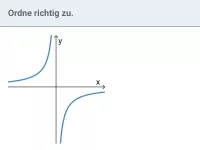
Was beschreibt die Funktionsgleichung und welche Eigenschaften hat der Graph einer Potenzfunktion mit negativem Exponenten?
Eine Funktion mit dem Term f(x) = a·x−n = a/xn (n natürliche Zahl, a≠0, x≠0) nennt man Potenzfunktion mit negativem Exponenten. Den zugehörigen Graphen nennt man Hyperbel der Ordnung n. Beachte:
- x- und y-Achse sind Asymptoten des Graphen Gf.
- Ist n gerade, so ist Gf symmetrisch zur y-Achse. Ist n ungerade, so ist Gf symmetrisch zum Ursprung des KOSY.
- Ist a positiv, so verläuft Gf u.a. durch den ersten Quadranten des KOSY, ansonsten durch den vierten.
Beispiel
Bestimme den Wert des Parameters \( a \) für die Potenzfunktion \( f(x) = a \cdot x^{-3} \), sodass ihr Graph durch den Punkt \( \left( \frac{1}{2}, 16 \right) \) verläuft.
- Setze den Punkt \( \left( \frac{1}{2}, 16 \right) \) in die Funktion \( f(x) = a \cdot x^{-3} \) ein: \[ f\left( \frac{1}{2} \right) = 16 \] \[ a \cdot \left( \frac{1}{2} \right)^{-3} = 16 \]
- Berechne \( \left( \frac{1}{2} \right)^{-3} \): \[ \left( \frac{1}{2} \right)^{-3} = \left( 2 \right)^3 = 8 \]
- Setze dies in die Gleichung ein: \[ a \cdot 8 = 16 \]
- Isoliere \( a \): \[ a = \frac{16}{8} \] \[ a = 2 \]
Also muss der Parameter \( a \) den Wert \( 2 \) haben, damit der Graph der Funktion \( f(x) = 2 \cdot x^{-3} \) durch den Punkt \( \left( \frac{1}{2}, 16 \right) \) verläuft.
Ergebnis:
Der Parameter \( a \) ist \( 2 \).
Siehe auch