Wie erkennt man beschränktes Wachstum und welche Formeln beschreiben es?

Sei B(n) der Bestand nach dem n-ten Zeitschritt. Beschränktes Wachstum liegt vor, wenn sich B(n) nach folgender rekursiven Formel berechnen lässt:

B(n + 1) = B(n) + c · [S − B(n)]

S drückt die Schranke des Wachstums aus, c das (konstante) Verhältnis von absoluter Zunahme und dem Sättigungsmanko S − B(n).

Schneller lässt sich B(n) oft mit folgender (nicht rekursiven) Formel berechnen:

B(n) = S − (1 − c)n · [S − B(0)]

Beispiel 1
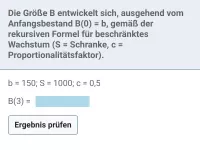
Die Größe B entwickelt sich, ausgehend vom Anfangsbestand B(0) = b, gemäß der rekursiven Formel für beschränktes Wachstum. Bestimme B für die ersten 3 Zeitschritte, wobei b = 1000; Schranke S = 5000; Proportionalitätsfaktor c = 0,4.
  • Lösung mit rekursiver Formel
Man fängt an mit B(0) = b = 1000. Die 2600 (darunter) ergibt sich durch Addition von 1000 und 1600. Dieses Verfahren wird wiederholt, bis man bei B(3) angekommen ist.
n
B
 
n
5000
−
B
 
n
·
0,4
0
1000
4000
1600
1
2600
2400
960
2
3560
1440
576
3
4136
  • alternative Berechnung
Mit Hilfe der nicht rekursiven Formel rechnet man z.B.
B
 
3
=
5000
−
0,6
3
·
5000
−
1000
=
5000
−
864
=
4136
Beispiel 2
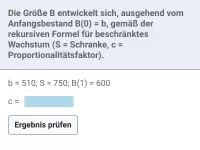
Die Größe B entwickelt sich, ausgehend vom Anfangsbestand B(0) = b, gemäß der rekursiven Formel für beschränktes Wachstum. Bestimme B(3), wenn bekannt ist: b = 600; B(1) = 780; Proportionalitätsfaktor c = 0,3.
Lösung:
  • Sättigungsgrenze S bestimmen
Bestimme zunächst S mit Hilfe der Rekursionsformel:
B
 
1
=
B
 
0
+
c
·
S
−
B
 
0
gegebene Werte einsetzen
780
=
600
+
0,3
·
S
−
600
nach S auflösen
780
=
600
+
0,3
·
S
−
180
+
180
780
=
420
+
0,3
·
S
−
420
360
=
0,3
·
S
:
0,3
1200
=
S
  • B(3) mit der rekursiven Formel bestimmen
Jetzt sind alle Parameter bekannt, um B(2), B(3) usw. zu bestimmen:
n
B
 
n
1200
−
B
 
n
·
0,3
1
780
420
126
2
906
294
88,2
3
994,2
  • alternative Berechnung von B(3)
Schneller geht es mit der nicht rekursiven Formel:
B
 
3
=
1200
−
0,7
3
·
1200
−
600
=
1200
−
205,8
=
994,2
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen