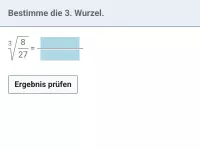
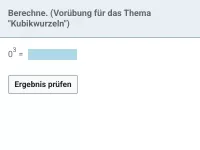
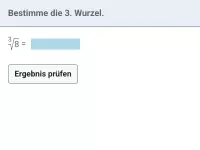
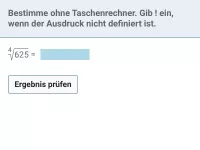
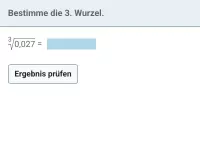
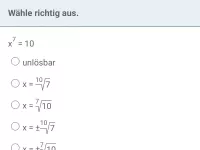
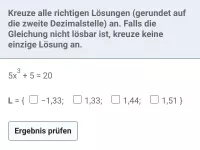
Wie viele Lösungen hat die Gleichung x^n=a (n ∈ N) in Abhängigkeit von a und n?
Die Gleichung xn=a (n ∈ N)
- hat KEINE Lösung, wenn n eine gerade Zahl ist und a<0.
- hat GENAU ZWEI Lösungen, wenn n eine gerade Zahl und a>0, nämlich die n-te Wurzel von a als auch deren Gegenzahl.
- hat GENAU EINE Lösung, wenn n eine ungerade Zahl und a>0, nämlich die n-te Wurzel von a.
- hat GENAU EINE Lösung, wenn n eine ungerade Zahl und a<0, nämlich die Gegenzahl der n-te Wurzel von |a|.
Beispiel
Löse, falls möglich:
| = |
|
| = | 5 |
| = | 5 |
| = |
|
| = | 0 |
Lösung:
a) keine Lösung, da
(gerader Exponent) nicht negativ sein kann.
x | 4 |
b) zwei Lösungen
| = |
|
c) eine Lösung
x | = |
|
d) eine Lösung
Achtung:
ist falsch; unter der Wurzel darf per Definition niemals eine negative Zahl stehen, auch nicht unter der dritten Wurzel!
x | = |
|
Achtung:
|
|
|
e)
x | = | 0 |

Lernvideo
POTENZGLEICHUNGEN lösen – GLEICHUNGEN mit geraden, ungeraden, rationalen, negativen Exponenten
Kanal: MathemaTrick
Siehe auch