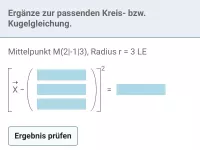
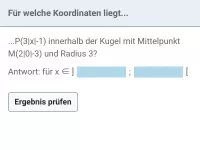
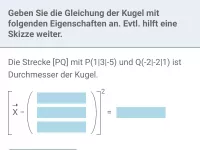
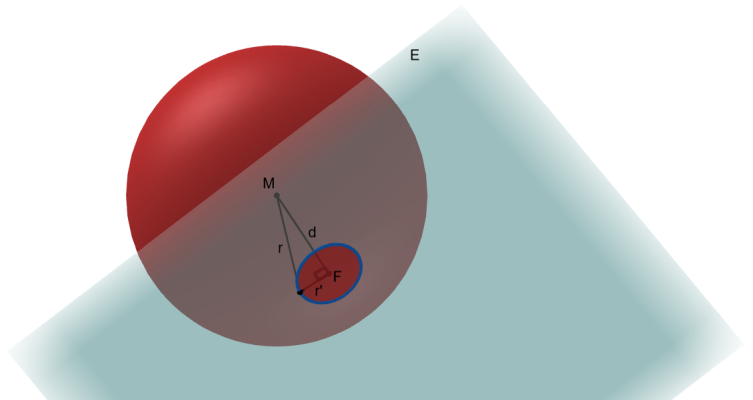
Gegeben ist eine Kugel k mit Mittelpunkt M und Radius r sowie eine Ebene E. Der Abstand d von M zu E gibt Aufschluss darüber, welcher der drei Fälle vorliegt:
- Im Fall d < r schneiden sich k und E, die Schnittmenge ist ein Kreis. Dessen Radius r' lässt sich mittels Pythagoras bestimmen: r²=d²+(r')²
- Im Fall d = r berühren sich k und E in einem Punkt (=Lotfußpunkt F des Lots von M auf E)
- Im Fall d > r haben k und E keine gemeinsamen Punkte.
Beispiel
Gegeben ist eine Kugel k mit dem Mittelpunkt M(1|−4|3) und dem Radius
sowie die Ebene
Stelle fest, ob k und E gemeinsame Punkte besitzen. Falls ja, bestimme den Berührpunkt bzw. Mittelpunkt und Radius des Schnittkreises.
r | = | 4,5 |
| = | 0. |
- Abstand d zwischen M und E
Die Gerade
die sich aus
als Stützvektor und dem ablesbaren Normalenvektor von E als Richtungsvektor zusammensetzt, ist Lotgerade von E durch M. Um den Lotfußpunkt F zu ermitteln, wird g in E eingesetzt:
|
|
M
| = |
| ||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||
| = |
|
| |||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||
Der Abstand d zwischen M und E beträgt damit:
| = |
|
- Lagebeziehung und gemeinsame Punkte
| = | 4,38…< 4,5, |
| r |
- Schnittkreis k' bestimmen
Der Mittelpunkt F des Schnittkreises ist Lotfußpunkt und ergibt sich durch Einsetzen von
in die Lotgerade g:
λ | = |
|
| = |
|
Der Schnittkreisradius r' ergibt sich aus r und d mit dem Satz des Pythagoras:
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
Siehe auch