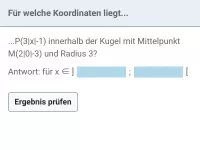
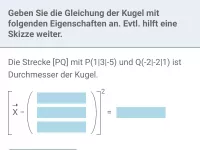
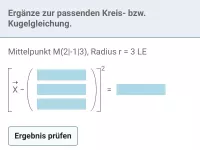
Wie liegen eine Kugel und eine Gerade zueinander und wie bestimmt man Berühr- oder Schnittpunkte?
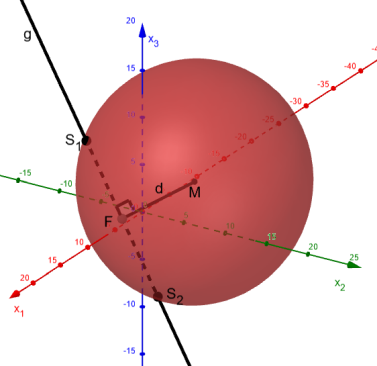
Gegeben ist eine Kugel k mit Mittelpunkt M und Radius r sowie eine Gerade g. Der Abstand d von M zu g gibt Aufschluss darüber, welcher der drei Fälle vorliegt:
- Im Fall d < r schneiden sich k und g in zwei Punkten. Die Schnittpunkte ermittelt man durch Einsetzen von g in k.
- Im Fall d = r berühren sich k und E in einem Punkt (=Lotfußpunkt F des Lots von M auf g)
- Im Fall d > r haben k und g keine gemeinsamen Punkte.
Beispiel
Gegeben ist eine Kugel k mit dem Mittelpunkt M(-5|3|2) und dem Radius
sowie die Gerade
r | = | 12 |
| = |
|
Ermittle, welchen Abstand der Kugelmittelpunkt M zur Geraden g hat und bestimme, soweit vorhanden, alle gemeinsamen Punkte von k und g.
- Abstand d zwischen M und g
Sei
ein beliebiger Punkt auf g, also
P | λ |
| = |
|
Man sucht nun unter der Schar der Vektoren
denjenigen, der senkrecht zu g steht und erhält damit den kürzesten Verbindungsvektor und damit den Abstand d zwischen M und g. Ansatz:
MP | λ |
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||
Der Abstand d zwischen M und g beträgt damit:
| = |
|
| = |
|
- Lagebeziehung und gemeinsame Punkte
8,072… < 12,
| r |
Die beiden Schnittpunkte erhält man durch Einsetzen von g in die Kugelgleichung von k. Arbeitserleichternd ist dabei die Verwendung des oben bestimmten Vektors
:
MP | λ |
| = |
| Einsetzen von g | |||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||
| = |
|
| |||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||
Jetzt kann man durch Einsetzen von μ in g die beiden Schnittpunkte ausrechnen:
| = |
|
| = |
|
Siehe auch