Wie entsteht ein Rotationskörper aus dem Graphen einer Funktion und wie berechnet man dessen Volumen?
Für eine stetige Funktion f, die in einem Intervall [a;b] definiert ist, kann man die Fläche zwischen dem Graphen von f und der x-Achse um die x-Achse rotieren lassen. Dadurch entsteht ein Rotationskörper, dessen Volumen V dem Integral über (f(x))² mit Untergrenze a und Obergrenze b, multipliziert mit π, entspricht.
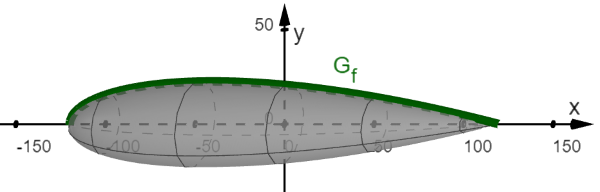
Die Abbildung zeigt ein ungefähres Modell des Luftschiffs Hindenburg, das am 6.5.1937 bei einem tragischen Unfall in Flammen aufging. Der dargestellte Körper kann aus dem Graphen der in definierten Funktion f mit gewonnen werden: Lässt man die Fläche unter um die x-Achse rotieren, so ergibt sich als Rotationskörper das Modell des Luftschiffs.
Ermittle, welches Volumen der Korpus der Hindenburg hatte, wenn eine Längeneinheit im Modell einem Meter in Wirklichkeit entspricht.
Da entspricht, beträgt das gesuchte Volumen
