Wie löst man Optimierungsaufgaben in der Mathematik?
Wenn es um die Optimierung einer bestimmten Größe geht, gehe wie folgt vor:
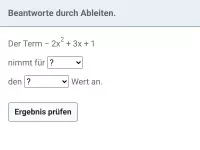
- Beschreibe die Größe, die möglichst groß oder möglichst klein werden soll (z.B. der Flächeninhalt einer Figur, das Volumen eines Körpers oder der Umsatz einer Ware) durch einen Term T, in dem die flexible Größe x (z.B. eine Seite der Figur oder des Körpers, der Preis der Ware) vorkommt.
- Falls weitere Variablen im Term vorkommen: Überlege dir, in welchem Zusammenhang sie zu x stehen. Stelle sie in Abhängigkeit von x dar und ersetze sie im obigen Term, so dass T nur noch von x abhängt. Überlege dir auch den Definitionsbereich von T(x).
- Bestimme jetzt mit den Werkzeugen der Infinitesimalrechnung (Ableitung etc.) die Stellen, an denen relative Extremata auftreten und beantworte damit die in der Aufgabe gestellten Fragen.
Beispiel 1
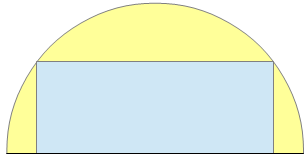
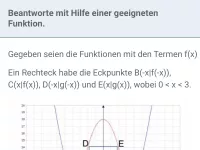
Der Halbkreis hat den Radius r. Bestimme die Seiten des einbeschriebenen Rechtecks (in Abhängigkeit von r) so, dass die Rechtecksfläche möglichst groß ist und gib den maximalen Flächeninhalt an.
Lösung siehe Video; im zweiten Video wird ein anderes Beispiel durchgerechnet.

Lernvideo
Differenzieren, Extremwertaufgabe, Flächenmaximierung
Kanal: Mathegym
Lernvideo
Extremwertaufgaben mit Funktionen – maximaler Flächeninhalt Rechteck unter Parabel
Kanal: MathemaTrick
Beispiel 2
Ein Spielzeughersteller setzt mit einem bestimmten Spielzeug, das er zu 35 € pro Stück verkauft, jährlich 280 000 € um. Eine Marktstudie zeigt, dass pro 1 € Preissenkung jeweils 1000 Stück mehr verkauft würden - sofern der Preis nicht unter 20 € fällt. Zu welchem Preis müsste das Spielzeug verkauft werden, um maximalen Umsatz zu erzielen?
Lösung siehe Video:

Lernvideo
Differenzieren, Extremwertaufgabe, Umsatzmaximierung
Kanal: Mathegym
Siehe auch