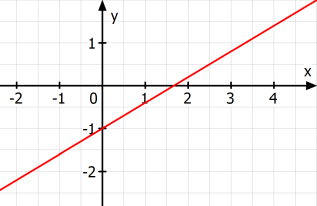
Lineare Funktionen - Ablesen am Graphen
Graphische Darstellung linearer Funktionen (Steigung und y-Achsenabschnitt), zeichnerische Schnittpunktbestimmung, graphisches Lösen von linearen Gleichungen, Textaufgaben
Lernvideo
Lineare Funktionen - Graph und Funktionsterm
Kanal: Mathegym
Jede lineare Gleichung mit zwei Variablen x und y kann als Gerade interpretiert werden. Jeder Punkt (x- und y-Koordinate) der Gerade stellt eine von unendlich vielen Lösungen dar.
Beispiel
| = | 1,8 |
Stelle diese Gleichung als Gerade dar und lies drei Lösungen ab.
Jede lineare Gleichung mit einer Unbekannten kann auch zeichnerisch gelöst werden: Die Terme links und rechts vom Gleichheitszeichen werden dabei als Geraden interpretiert (y = ...). Zeichne die Geraden ein und schaue, ob und - wenn ja - wo sie sich schneiden.
Beispiel
Löse durch Zeichnung:
a)
| = |
|
b)
| = |
|
Beispiel
Dirk wiegt 72 kg und möchte mit Krafttraining Muskelmasse aufbauen, um Wrestler im Superschwergewicht zu werden. Mit Hilfe eines strengen Trainings- und Ernährungsplans will er pro Monat ca. 5kg zulegen. Sebastian hat mit 102kg deutlich Übergewicht und will durch eine disziplinierte Diät wöchentlich ca. 500g abnehmen. Nach wie vielen Wochen wären Dirk und Sebastian gleich schwer, wenn sie mit der Umsetzung ihrer Pläne zur selben Zeit beginnen und durchhalten?
Die Steigung m einer Geraden verrät durch ihr Vorzeichen, ob die Gerade steigt (m>0) oder fällt (m<0). Sonderfall: waagrechte Gerade (m=0). Am Betrag vom m sieht man, wie steil die Gerade verläuft. Je größer |m|, desto steiler die Gerade.
Liegt die Gerade als Zeichnung vor, kann man ihre Steigung m als Bruch angeben. Wähle dazu zwei beliebige Punkte auf der Geraden aus und zähle ab, wie viele Kästchen du vom linken Punkt aus nach rechts (⇒ Nenner von m) und von dort aus nach oben oder unten gehen musst (⇒ positiver bzw. negativer Zähler von m), um beim rechten Punkt anzukommen.
Beispiel
Bestimme die Steigung der Geraden.