Bessere Noten in Mathe

Mit Spaß und Motivation lernen und üben

Verpassten Lernstoff aufholen

Optimal auf die nächste Prüfung vorbereiten

Bessere Noten schreiben
Mathe
Latein
Englisch
Chemie
Physik
Mathe online üben und lernen
Dein smarter Mathe-Trainer
Ab
4.92€
pro Monat
Wir machen dich fit in Mathe! Auf spielerische Art und Weise, in deinem eigenen Tempo. Vielen Schülern macht es richtig Spaß, mit Mathegym zu üben und an den interaktiven Online-Aufgaben zu knobeln.
- Bei uns findest du zahlreiche Mathe-Aufgaben, Hilfestellungen, ausführliche Lösungen und Lernvideos zu fast allen Themen der Schulmathematik in den Klassen 5-13, passend zum Lehrplan in deinem Bundesland.
- Komplexe Aufgaben können Schritt für Schritt gelöst werden.
- Ist das Ergebnis falsch, gibt dir das Programm oft wertvolle Hinweise, wie sich der Fehler korrigieren lässt.
Wenn Mathe, dann Mathegym!
-
Kompetent in Mathe
Alle Aufgaben und Lösungen stammen von praktisch erfahrenen Lehrkräften. -
Mehrfach prämiert
Mathegym wurde bereits mehrfach ausgezeichnet, von Wissenschaftlern, Pädagogen, Psychologen und Fachjournalisten. Infos dazu -
An 478 Schulen im Einsatz
Unsere Lernplattform überzeugt inzwischen auch schon 478 Schulen, die Mathegym lizenzieren und zum Üben einsetzen.
Mathegym auf einen Blick
Interesse an den vielfältigen Funktionen von Mathegym? Klicke auf die einzelnen Punkte, um einen schnellen Überblick zu bekommen, wie du mit Mathegym in Mathe durchstarten kannst.

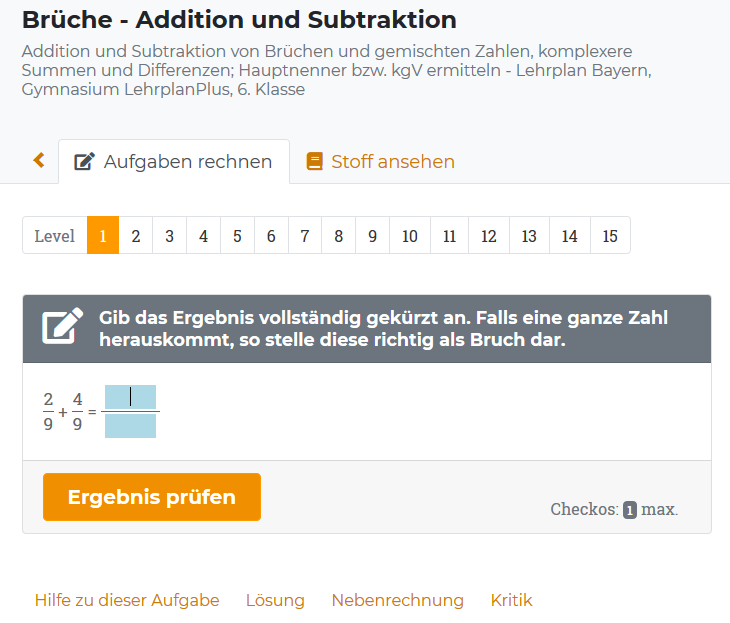
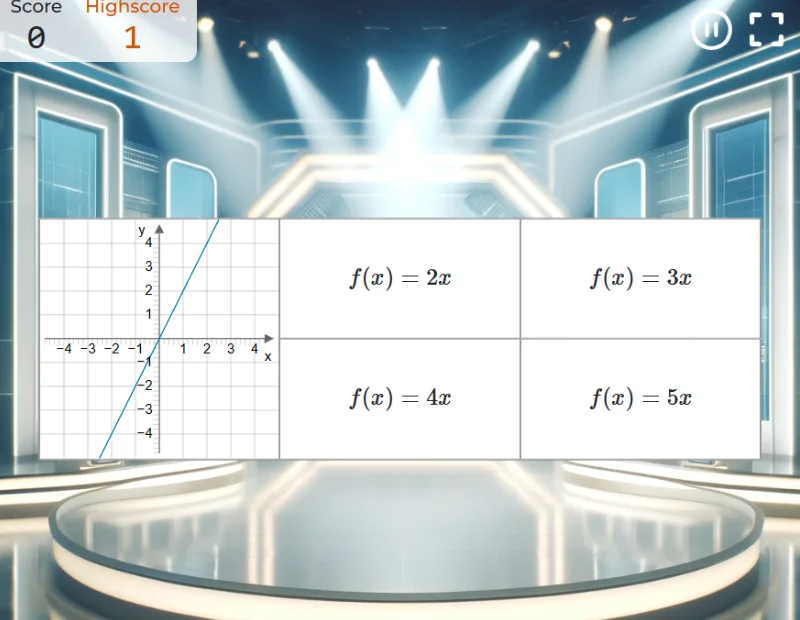
Der Aufgabenbereich
- Hier findest du zahlreiche Online-Übungen, Hilfestellungen, ausführliche Lösungen und Lernvideos zu fast allen Themen der Schulmathematik in den Klassen 5 bis 13, passend zum Lehrplan in deinem Bundesland.
- Am Anfang stehen immer leichte Aufgaben. Je nach Erfolg steigert sich der Schwierigkeitsgrad.
- Hinter jedem Level (hier 1-15) verbergen sich mehrere ähnliche Aufgaben - ideal, um Sicherheit bei einem Aufgabentyp zu erwerben.
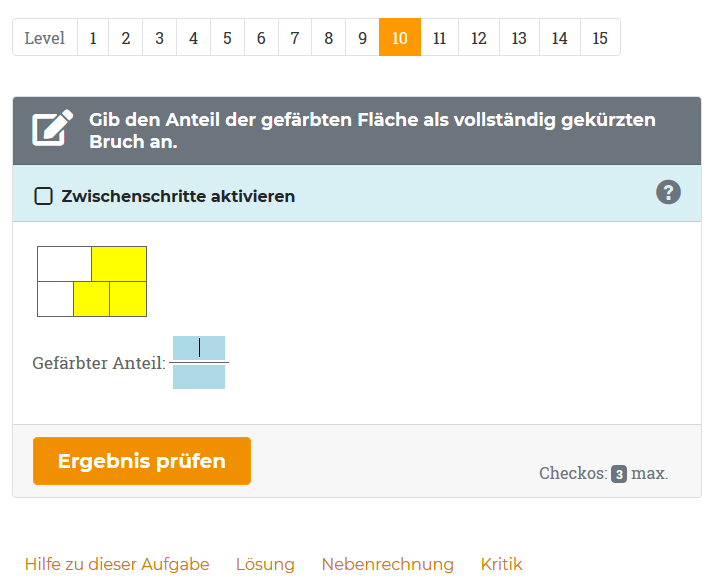
- Komplexe Aufgaben können auch Schritt für Schritt gelöst werden.
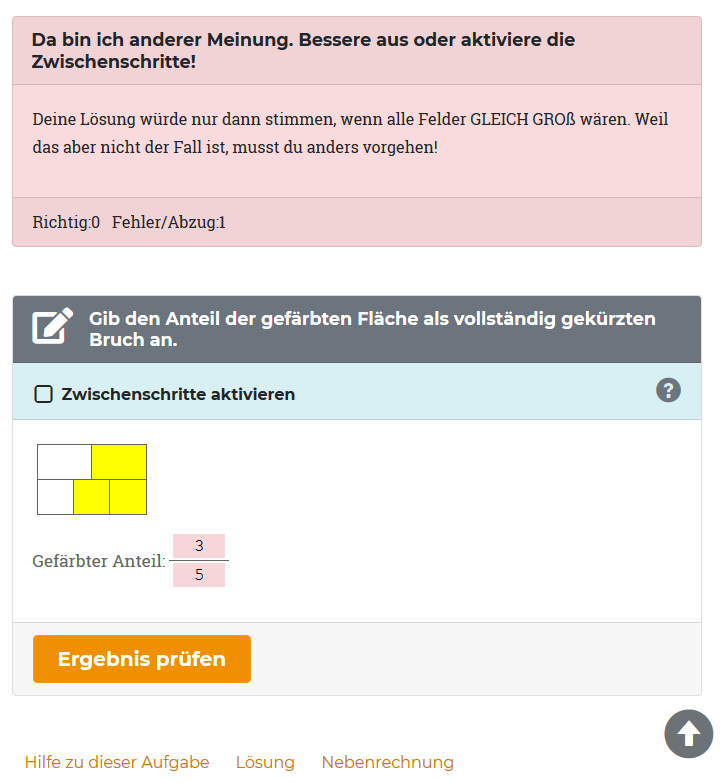
- Ist das Ergebnis falsch, gibt dir das Programm oft wertvolle Hinweise, wie sich der Fehler korrigieren lässt.
- Zu jeder Aufgabe gibt es meistens eine Hilfestellungen und eine ausführliche Musterlösung.
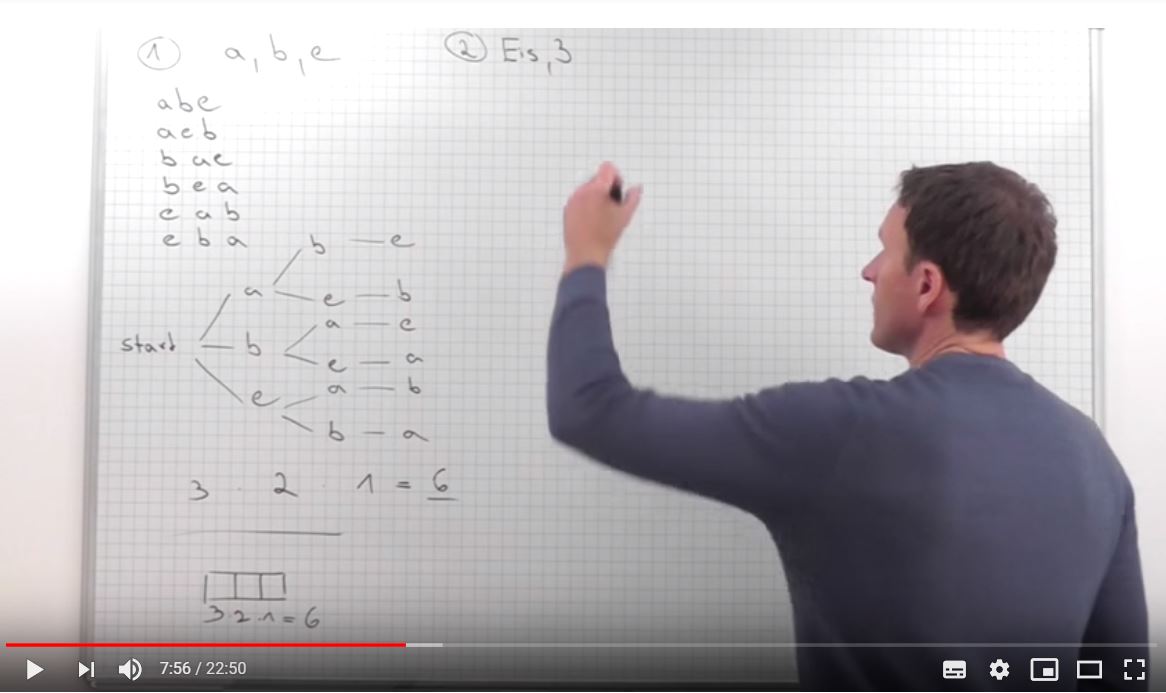
Video-Tutorials
- Der Übungsbereich wird ergänzt durch viele Video-Tutorials, in denen Beispielaufgaben vorgerechnet werden.
- Eine tolle Hilfe, um versäumten oder noch nicht verstandenen Stoff zu Hause eigenständig nachzuholen.
- Klicke auf das nebenstehende Bild, um dir ein Beispiel-Lernvideo anzusehen.
Adaptives Lernsystem
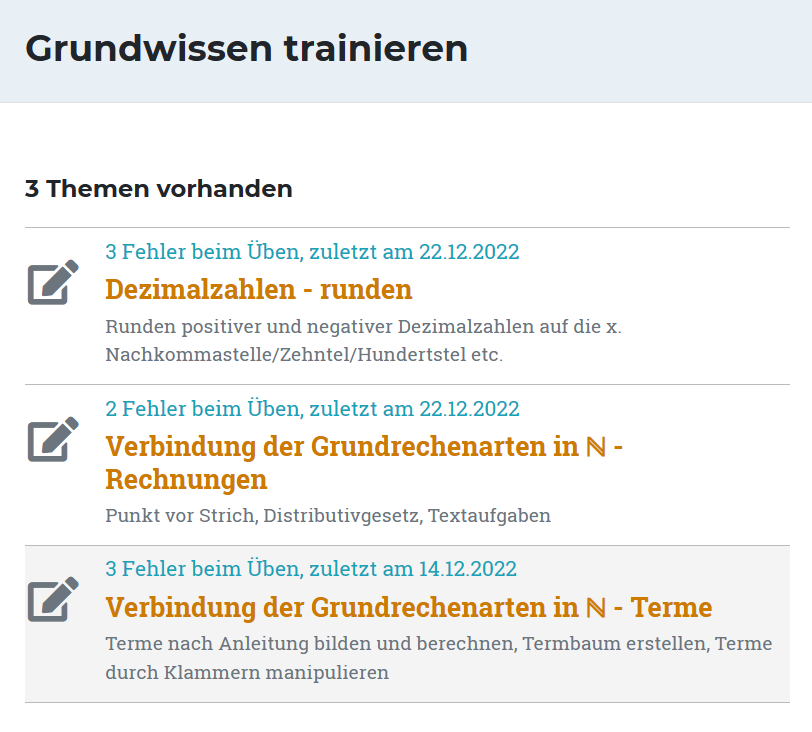
- Beim Lösen der Aufgaben erkennt unser System spezifische Lücken in deinem Grundwissen und stellt dir passgenaue Übungen zusammen, die du im Bereich "Grundwissen trainieren" abrufen kannst.
- Du erhältst damit die Chance, gezielt an deinen Schwächen zu arbeiten und deine Wissenslücken nach und nach zu schließen.
Checkos sammeln, Top-30-Listen
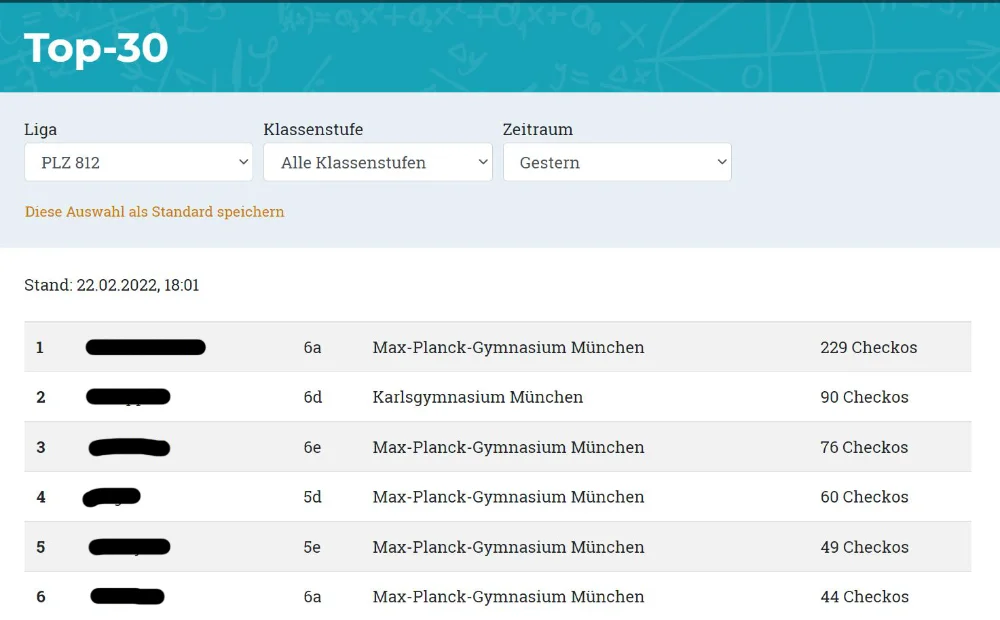
- Für richtige Lösungen erwirbst du Belohnungspunkte, sogenannte "Checkos".
- Damit kannst du in Ranglisten aufsteigen. Neben einer Gesamtrangliste gibt es lokale Ranglisten, z. B. auf die eigene Schule, Klassenstufe oder Klasse bezogen.
- Hinweis: Die Teilnahme an den Ranglisten ist optional und kann jederzeit deaktiviert werden.
Lernspiele
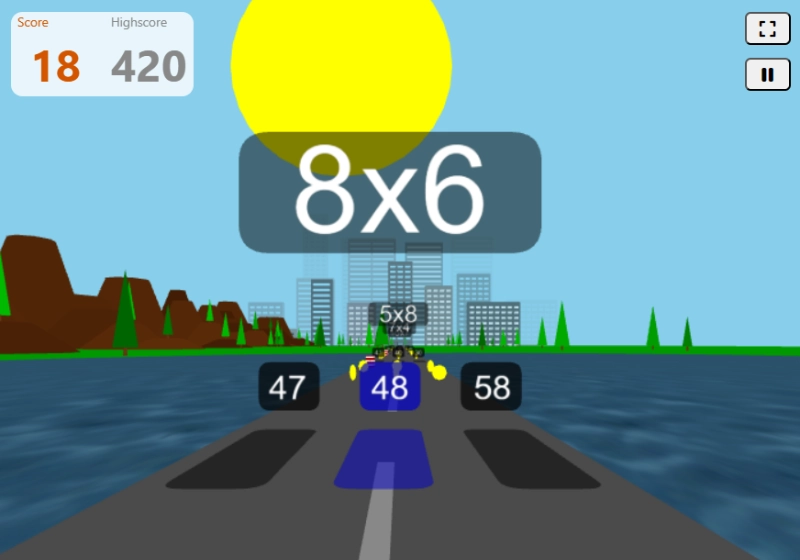
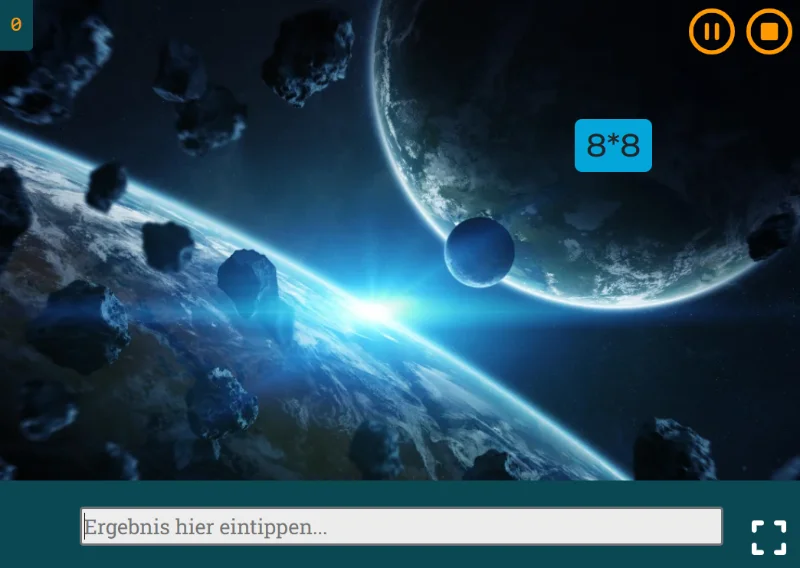
- Vokabeln und Kopfrechnen gehören zu den Dingen, die viel Wiederholung erfordern - das kann schnell mal langeweilig werden. Unsere Online-Lernspiele sorgen dafür, dass es spannend bleibt und helfen spielerisch, das Gelernte zu festigen.
- Für Schüler, die eine Pause vom Lernen benötigen, eine willkommene Abwechslung.
- Motivation spielerisch fördern.
So üben und lernen Schüler mit Mathegym
In diesem Video stellen dir Marlene und Benedikt den Aufgabenbereich von Mathegym vor. Sie erklären dir, wie du passende Online-Übungen findest und wie du die vielen Hilfen, die unsere Lernplattform bietet, bestmöglich für dich nutzt.
Die Vorteile für Sie als Eltern
Bei uns ist Ihr Kind in besten Händen. Das belegen mehrere wissenschaftliche Studien, zahlreiche Auszeichnungen und 478 Schulen, die ihre Schüler mit Mathegym üben lassen.
- Mathegym hilft Ihrem Kind motiviert und selbstständig zu lernen und unterstützt es bei der Prüfungsvorbereitung.
- Mathegym entlastet Sie als Nachhilfeassistent beim täglichen Mathelernen zu Hause.
- Der Schulstoff wird von erfahrenen Lehrkräften motivierend erklärt und trainiert.
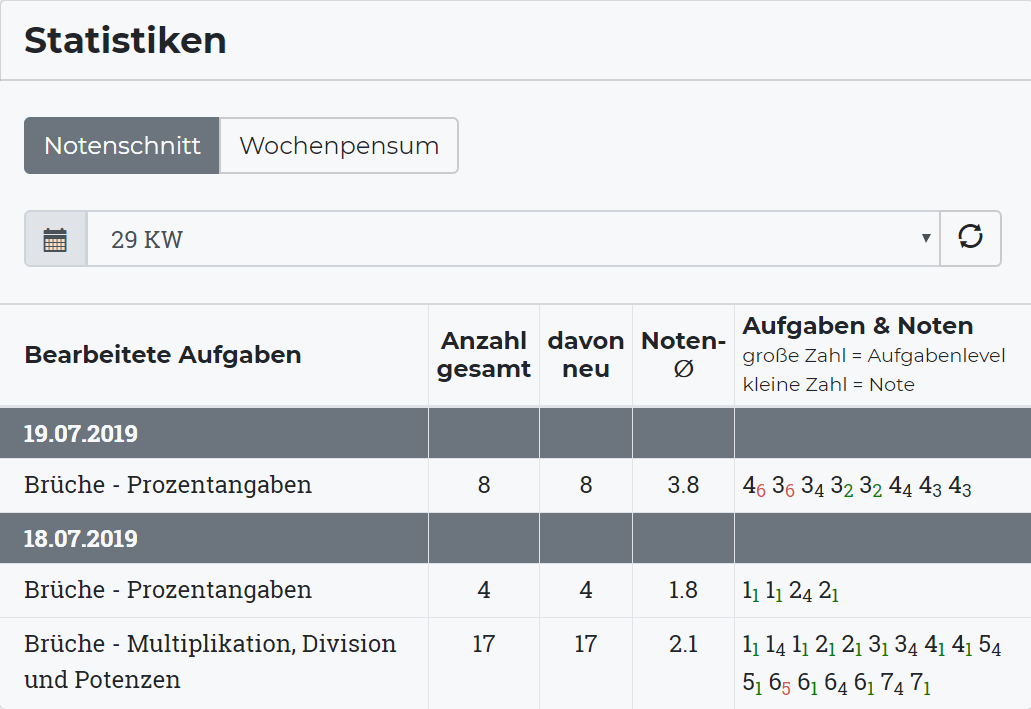
- Auf Wunsch können Sie sich wöchentlich per E-Mail über die Lernerfolge Ihres Kindes informieren lassen.


Mathe online üben und lernen
Unkompliziert testen, ohne Verpflichtung oder Vertragsbindung! Du erhältst sofort kostenlos Zugriff auf alle unsere Aufgabenbereiche und Fächer: Mathe, Latein, Englisch, Chemie und Physik.
Ohne Registrierung
- Zugang zu allen Aufgaben im 1. Level
oder
oder
Mit kostenloser Registrierung
- Zugang zu allen Aufgaben im 1. Level
- Zugang zu allen Aufgaben im 2. Level
- Checkos für richtig gelöste Aufgaben sammeln
Keine Verpflichtung: Dein Konto wird nach einem Monat automatisch gelöscht, sofern du es nicht auf Lizenzbasis weiterführen möchtest.