- y = x²:
Normalparabel mit Scheitel S im Ursprung
- y = (x + 2)²:
Um 2 nach links (bei "x − 2" nach rechts) verschobene Normalparabel, also Scheitel S(-2|0)
- y = x² + 2:
Um 2 nach oben (bei "x − 2" nach unten) verschobene Normalparabel, also Scheitel S(0|2)
- y = (x − 1)² + 3:
Um 1 nach rechts und um 3 nach oben verschobene Normalparabel, also Scheitel S(1|3)
Diese Zusammenhänge gelten auch, wenn ein Faktor vor x² bzw. (...)² steht.
Gib die Koordinaten des Scheitels an.
Um zu überprüfen, ob ein Punkt (a|b) über, auf oder unter dem Graphen einer Funktion liegt, setzt man a in den Funktionsterm f(x) ein. Der Punkt liegt
- über dem Graphen, wenn b > f(a)
- auf dem Graphen, wenn b = f(a)
- unter dem Graphen, wenn b < f(a)
Gib jeweils an, ob der der Punkt über, auf oder unter der Parabel liegt.
- Der Scheitelpunkt einer Parabel gibt an, wo die zugehörige Funktion ein Maximum/Minimum hat und wie groß dieses ist. Wenn xS die x-Koordinate und yS die y-Koordinate des Scheitels ist, so hat die Funktion an der Stelle xS das Maximum bzw. Minimum yS.
- Bei einer nach oben geöffneten Parabel liegt ein Minimum, bei einer nach unten geöffneten Parabel ein Maximum vor.
Eine Parabel mit der Gleichung y = ax² + bx + c (Allgemeine Form) und dem Scheitel S(s ; t) lässt sich auch durch die Gleichung y = a (x − s)² + t (Scheitelpunktform) ausdrücken.
Weiß man, dass eine Parabel die x-Achse an den Stellen x
1 und x
2 schneidet, so kann man ihren Scheitel S leicht bestimmen:
- xS = (x1 + x2) : 2
Begründung: xS (also die x-Koordinate des Scheitels) liegt aus Symmetriegründen genau in der Mitte des Intervalls [x1 ; x2]
- yS = p(xS)
d.h. die y-Koordinate erhält man durch Einsetzen von xS in den Funktionsterm der Parabel
Die Parabel mit der Gleichung schneidet die x-Achse an den Stellen und . Bestimme die Koordinaten des Scheitelpunkts.
In einer Wertetabelle sind x- und y-Werte einander gegenübergestellt. Die Wertetabelle erhält man, indem man vorgegebene x-Werte in den Funktionsterm einsetzt und so die zugehörigen y-Werte ausrechnet. Die (x|y)-Paare sind Punkte des Grafen.
Eine Gleichung kann graphisch gelöst werden, indem man beide Seiten der Gleichung als Funktionsterm betrachtet und die zugehörigen Graphen zeichnet. Die Stellen, wo sie sich schneiden bzw. berühren, sind die Lösungen der Gleichung. Keine gemeinsamen Punkte dagegen heißt keine Lösung.
Die durch y = ax² (a≠0) definierte Parabel hat den Scheitel im Ursprung und ist gegenüber der Normalparabel in y-Richtung um das |a|-fache gestreckt (|a|>1) oder gestaucht (|a|<1). Das Vorzeichen von a legt fest, ob die Parabel nach oben (a positiv) oder nach unten (a negativ) geöffnet ist.
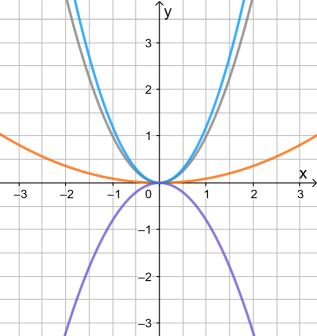
Neben der Normalparabel (grau) sind drei verschiedene Parabeln mit der Gleichung y = ax² dargestellt. Lies jeweils das Vorzeichen von a ab und gib an, ob |a|>1 oder |a|<1.
Man unterscheidet bei einer Parabel zwischen
- Allgemeiner Form y = ax² + bx + c ⇒ Ablesen des Schnittpunkts mit der y-Achse (0;c)
- Scheitelpunktform y = a (x - xS)² + yS ⇒ Ablesen des Scheitels S
Von der allgemeinen Form ausgehend erhält man die Scheitelpunktform mithilfe der quadratischen Ergänzung.
Bringe in Scheitelpunktform und gib den Scheitel an.
Durch die Gleichung
y = a⋅(x - xS)² + yS (a≠0) ist eine Parabel mit den Scheitelkoordinaten
xS und
yS gegeben, die gegenüber der Normalparabel mit der Gleichung
y = x²
- nach unten geöffnet ist, falls a negativ ist und
- evtl. gestreckt (falls |a|>1) bzw. gestaucht (falls |a|<1) ist.
Abgebildet ist die Parabel mit der Gleichung
Die Gleichung einer Parabel sei bis auf den Formfaktor a bekannt. Dann lässt sich a bestimmen, indem man einen Punkt des Graphen aus dem Koordinatensystem abliest, ihn in die Parabelgleichung einsetzt und die Gleichung nach a auflöst.
Eine Parabel lässt sich durch drei geeignete Punkte eindeutig festlegen. Durch das Einsetzen der drei Punkte in die Funktionsgleichung y = ax² + bx + c erhält man ein Gleichungssystem mit den drei Unbekannten a, b und c. Dieses kann mittels Einsetz- oder Subtraktionsverfahren gelöst werden.
Ermittle die Gleichung der Parabel durch folgende Punkte: